ZKY-002
[Paper] VQRAE: Representation Quantization Autoencoders for Multimodal Understanding, Generation and Reconstruction
RAE
考虑不使用最原始的 SD-VAE 作为 diffusion 的 autoencoder,而是使用一些包含 representation 信息的 autoencoder(例如 DINO, MAE, SigLIP)。论文将这类 Encoder 称作 RAE。
论文使用了 Dino v2-B 作为 RAE,效果最好。
VQRAE
动机
在目前的 MLLM 中,模型的理解和生成通常使用的是两套不同的框架。VQRAE 希望能够将理解和生成统一到一套框架下,且兼顾如下性质:
- 理解(Visual Understanding)时能够利用 Visual Foundation Model 的 continuous semantic features。
- 生成图片时可以使用 discrete tokens 来生成。
Architecture & MLLM Usage
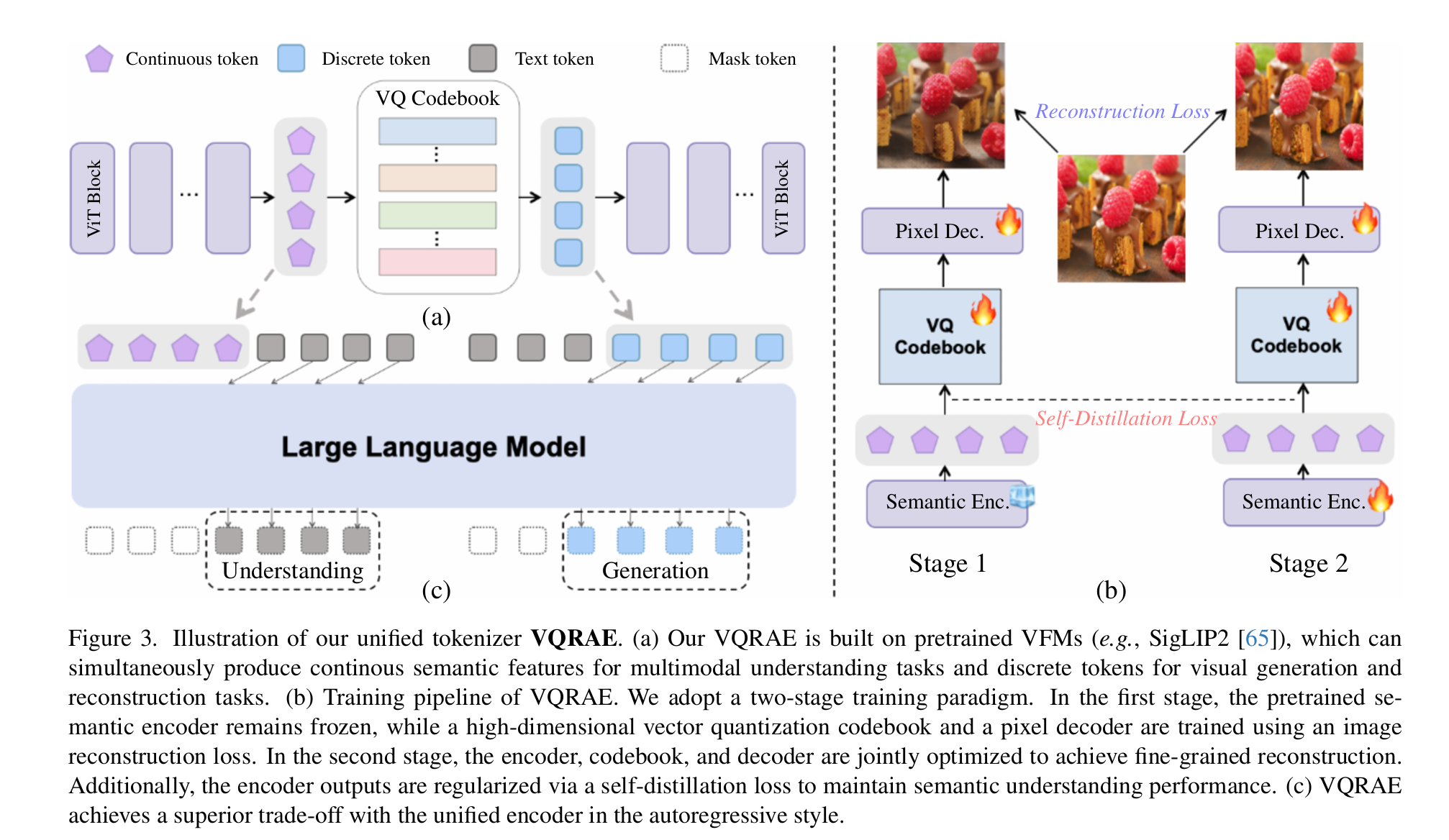
思路
VQ 的思想是将图片转换成一个离散的 Token 序列,我们就可以使用类似 LLM 的 Next Token Prediction 的目标。
我们训练 Encoder $E$,VQ codebook $C$,和一个 Decoder $D$。
在给图片 $x$ 过了 Encoder $E$ 之后,我们将 Encoder 的每个 token $e_i$ 投影到和 $q_i$(来对齐 Codebook 的维度),然后在 codebook $C$ 里面找到最接近的 $p_i:=argmin_{j}\mid \mid c_j-q_i\mid \mid $。这样我们就可以把这些 $q_i$ 量化成 $c_{p_i}$。我们希望解码时用 $D(c_{p_i})$ 能得到原来的图片 $x$ 。
之前的 VQ 方法常常在语义方面不够出色。因此,论文提出了 VQRAE,就是 VQ 版本的 RAE。VQRAE 使用了从 pre-trained VFM(vision foundation model) 开始训练的模型 Encoder $E$,和一个与 Encoder 架构相同的 symmetric ViT Decoder $D$。训练分为两个步骤。
Stage 1
我们 freeze 住 VFM Encoder,我们同时训练 CodeBook 和 Decoder,同时保证 CodeBook 的 semantic 属性和 decoder 的 reconstruction 属性。
\[\mathcal L_{\text{stage1}}=\mathcal L_{rec}+\mathcal L_{quant}\]- 设 $x’=D(c_{p_i})$,那么 $\mathcal L_{rec} = \mathcal l_2(x’,x)+\mathcal L_{\text{LPIPS}}(D(x,x’))+\lambda_G\mathcal L_{G}(x’)$。
- $\mathcal L_{quant}$ 是 SimVQ Loss,我们后面会提及它的实现。
Stage 2
Unfreeze VFM,并直接使用原来的 VFM 来算 self-distillation loss 以保持 VFM 的 semantic 属性,同时保持原来的 reconstruction loss 和 quant loss。
\[\mathcal L_{\text{stage1}}=\mathcal L_{rec}+\mathcal L_{quant}+\lambda_d\mathcal L_{distill}\]- 其中 $\mathcal L_{distill} = \mid \mid E(x) - E_0(x)\mid \mid ^2$,其中 $E_0$ 是最开始的被 freeze 住的 VFM。
SimVQ Loss
最原始的 VQ 训练方法就是直接训练一些随机初始化的“Parameters” $c_j$,然后按照 $\mathcal L = \min_j(\mid \mid q_i-c_j\mid \mid ^2)$ 对 $c$ 做梯度下降。这等价于在 argmin 位置加入 Loss $\mathcal L = \mid \mid q_i-c_{p_j}\mid \mid ^2$。
SimVQ 在此基础上做出了改进,极大地提升了 VQ Codebook 的利用效率:训练一个矩阵 $W$ 和一些 $c_{j}’$,然后令 $c_j = Wc_{j}’$。
接着同样按照 $\mathcal L=\min_{j} (\mid \mid q_i-c_j\mid \mid ^2)$ 梯度下降。其中矩阵 $W$ 是 $d\times d$ 的方阵,不改变 $c$ 的维度。
不同之处就在于 $W$ 也收获了梯度,这样一个 $c_i$ 可以在没有被梯度影响时做出更新,这样 $W$ 就给这些 $c_i$ 提供了不错的 “inductive bias”。
训练过程中,当 $q$ 也是 unfreeze 的时候,我们希望 $q_i$ 和 $c_j$ 以不同的速度相互靠近:我们更希望 $q_i$ 来靠近 $c_j$,而不是去改变 $c_j$。因此我们实际上会使用:
\[\mathcal L_{quant}=\mid \mid sg(c_{p_j})-q_i\mid \mid ^2+\beta \mid \mid c_{p_j}-sg(q_i)\mid \mid ^2\]其中 $\beta$ 取 $0.25$。
实验结果
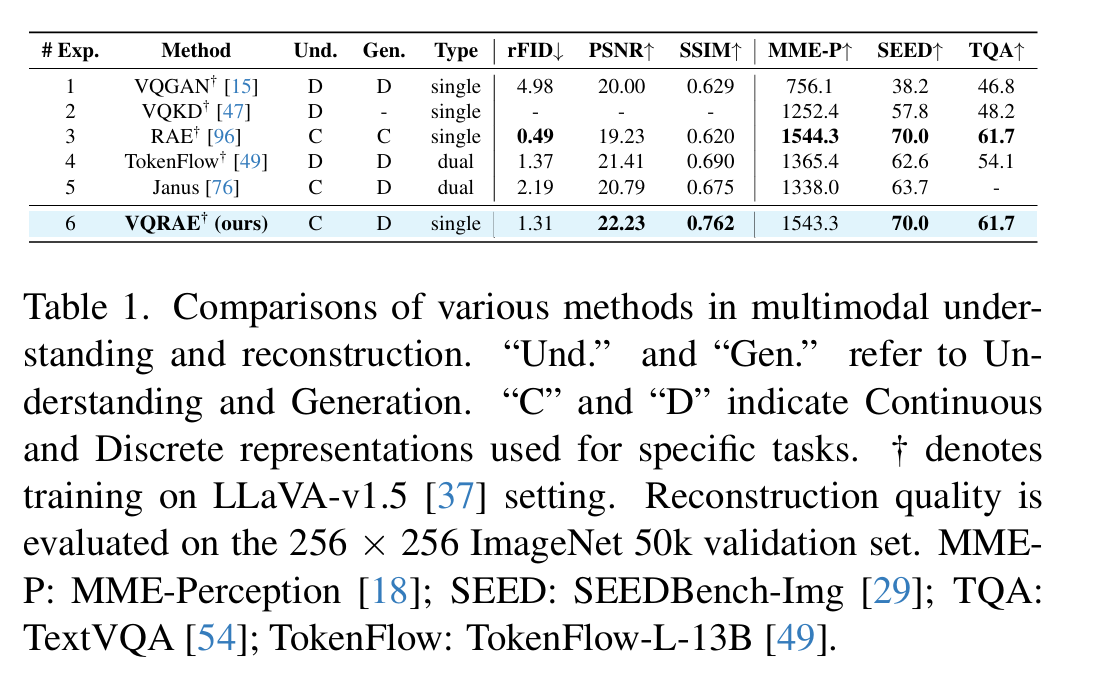
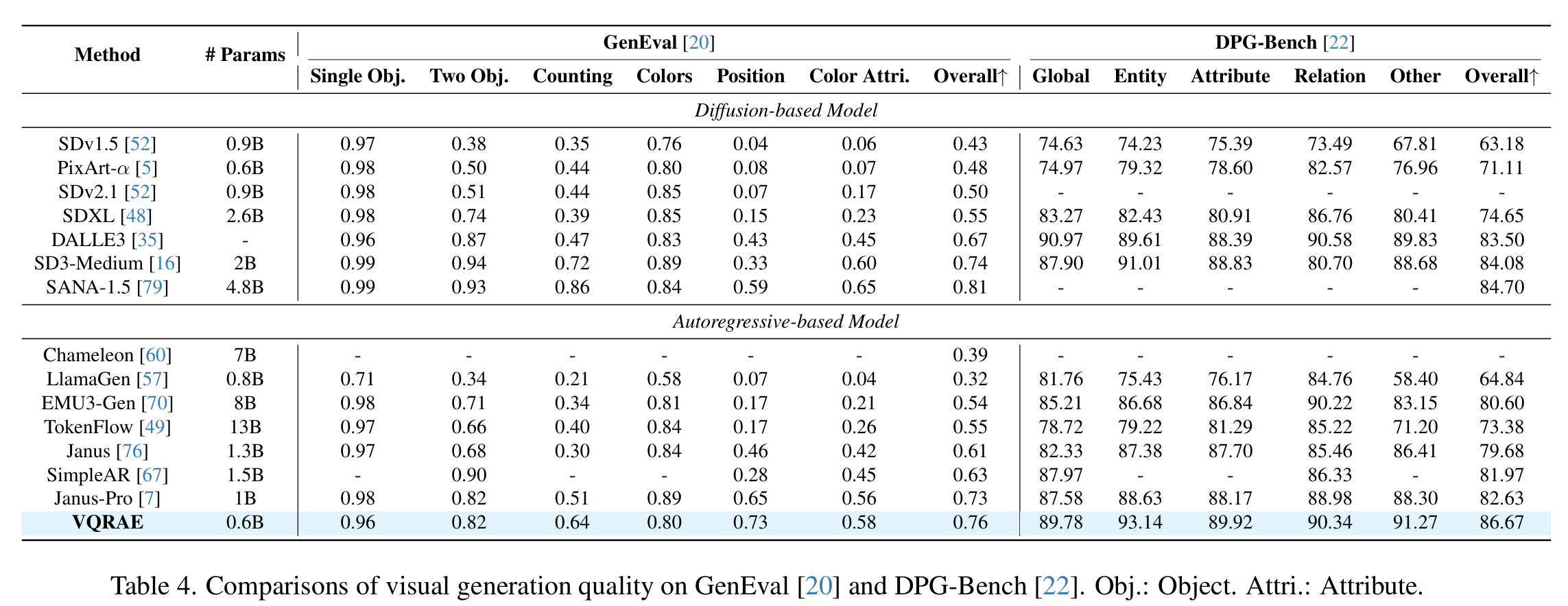
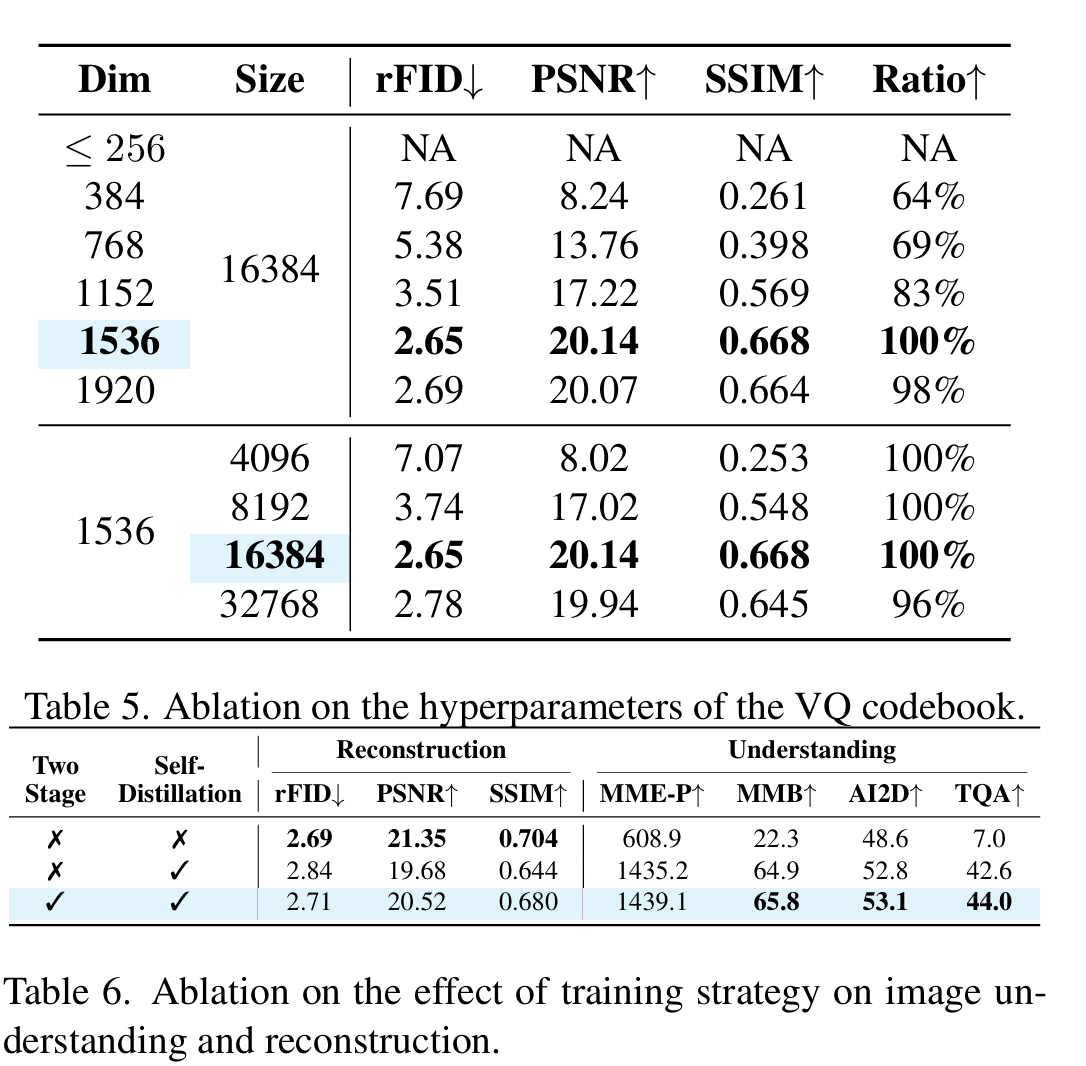
- Dim 是 Codebook Dim。之前工作的 VQ 为了生成好 details,通常采用 $8\sim 256$ 的 Dim,而 VQRAE 在 Dim 达到 $1536$ 的时候也可以保证很高的词表利用率。
- Size 是 Codebook 大小。
- Ratio 是 codebook utilization ratio,即被使用过的 code $c_i$ 的比例,可以发现 VQRAE 在较大的 Dim 下能够获得非常高的 ratio。