考虑 Gated Layer: 输入 $x\in \mathbb R^{d’}$ 和 $y\in \mathbb R^{d}$，输出定义为

\[\text{GatedLayer}_\theta(x,y) = y\odot \sigma(W_\theta x),\]

其中 $W_\theta \in \mathbb R^{d\times d’}$ 是可学习参数，$\sigma$ 是 sigmoid 函数。

我们将 Gated Layer 应用到 attention 机制中：$x$ 用 layer normalize 过后的 hidden state；$y$ 的选择很多样，可以是 $q,k,v$ 中的任意一个，或者做完 SDPA 之后的输出。如下图。

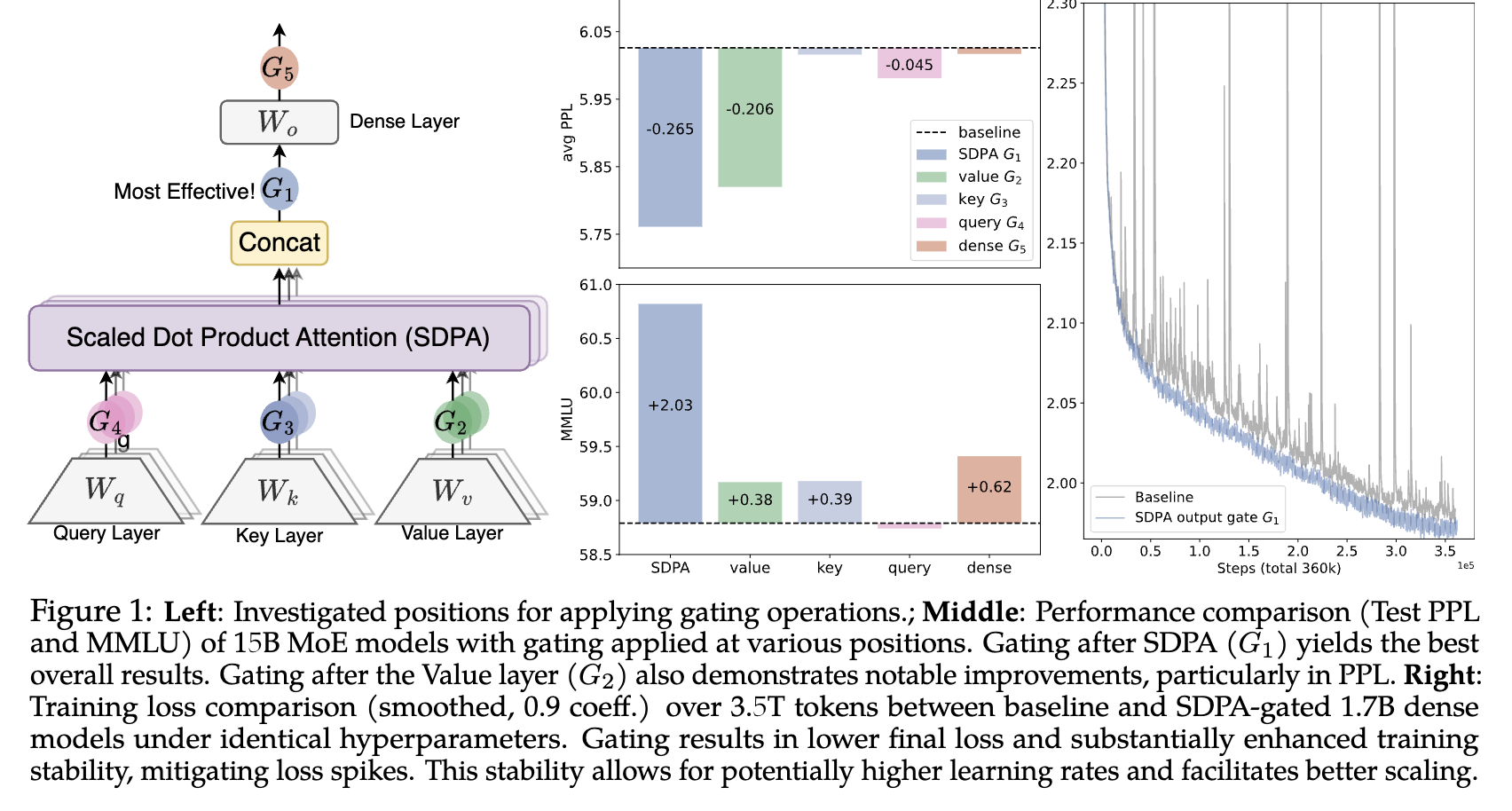
image not found

实验发现，apply 到 $v$ 和 SDPA 输出上效果显著好于其他位置。并且发现 training stability 明显提升，能够使用更大的 learning rate，从而得到更好的 performance。

Ablations

  • 我们 不能在 $W_\theta$ 上剩参数。如果每个 head 使用相同的 modulate weight，性能不会比 baseline 好很多。
  • 如果我们把 Gated Layer 换成 $y+\sigma(W_\theta x)$，会略掉点，但仍有显著提升。
  • Activation 选 sigmoid 会好于 SiLU；也可以直接把 gated layer 换成一层 RMSNorm (prior work)，也有类似的效果。
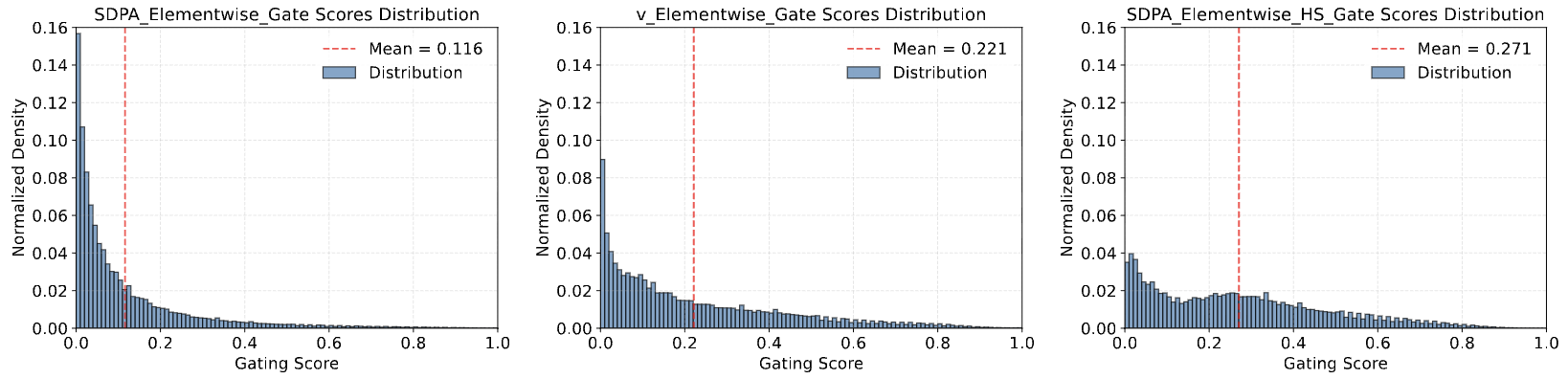
  • 如果把每一层的 $\sigma(\cdot)$ 的分布输出，发现是靠近 $0$ 的分布平均值约为 $0.11\sim 0.25$。 image not found

  • 于是我们把 sigmoid 换成

    \[\sigma_{0.5}(x)=0.5+0.5\cdot \sigma(x),\]

    也即强制让 weight $>0.5$，发现效果变差。并且 ablation 中 sparsity 和 performance 基本是反比关系。说明 sparsity is key。

  • About Attention Sink: 假如我们在 SDPA 后面加 gated layer，attention sink 现象很大缓解了，并且让 activation 更加 smooth 了 (改善 BF16 training; baseline 存在 massive act. 问题)。如果在 $v$ 上加，activation 也改善了，但是 attention sink 现象 并没有得到改善。

Theories

我们考虑第 $k$ 个 head 对序列第 $i$ 个 token 的贡献 $o_{i}^k$。

假设 $W_V^k, W_O^k$ 分别是第 $k$ 个 head 的 value matrix 和 output projection，${S_{ij}^k}_{i,j\le L}$ 是 attention score matrix，我们有

\[o_i^k = \sum_{j=1}^{i} S_{ij}^k \cdot (W_O^kW_V^k h_j).\]

我们立即发现 $W_OW_V$ 可以合成一个大的 matrix。因为每个 head 的 dimension 小于 activation dimension，所以 $W_OW_V$ 是一个 low-rank matrix。但即便如此，两个连续的 linear 总归还是影响表现力。

有两个 straightforward 的引入 non-linearity 的方法：第一个是

\[o_i^k = \sum_{j=1}^{i} S_{ij}^k \cdot (W_O^k\cdot \text{non-linearity}(W_V^k h_j)),\]

第二个是

\[o_i^k = W_O^k\cdot \text{non-linearity}\left(\sum_{j=1}^{i} S_{ij}^k \cdot (W_V^k h_j)\right).\]

第一个对应在 $v$ 上加 non-linearity，第二个对应在 SDPA 输出上加 non-linearity。

从这个视角来看，这个非线性函数贡献有两处：

  1. 提升表达能力；
  2. 如果它是 bounded function (比如 sigmoid)，它能引入 sparsity，并且起到 smooth weight 的作用。

从这里也能看出第一个没有直接解决 attention sink 的原因，因为 attention score 仍然是原始的 softmax distribution，没有被 modulate。