Background

Policy Gradient

比较熟悉或者不想看可以先跳过

本文中我们的 loss 都定义为 gradient ascent 的目标 (越大越好)

首先我们的 objective 是

\[\mathbb E[r_t]\]

其中，期望对我们的 policy 采样，以及对 $t$ 的采样。这里我们可以简单考虑先只考虑一个时间步骤

注意到我们需要对 policy $\pi$ 进行优化, 但是采样不能传梯度。目标可以进一步写成

\[\int \pi(a_t\mid s_t) r_t da_t\]

然后考虑这个东西的梯度就是 (叫做 policy gradient)

\[\int \nabla_{\theta}\pi(a_t\mid s_t) r_t da_t=\mathbb E[\nabla_{\theta}\log \pi(a_t\mid s_t) r_t]\]

于是我们只需要最大化下面的目标：（其中采样不传播梯度） $\mathbb E[\log \pi(a_t\mid s_t) r_t]$ 更进一步，我们可以把 $r$ 替换成 advantage $A_t$ (具体是减去一个常数不变). 这样方差更小/更直观. $\mathbb E[\log \pi(a_t\mid s_t) A_t]$ 这个式子的直观理解就是，当 $A_t$ 大于 0 的时候，我们增大这个 action 的概率，否则减小。log 的原因是，比如有一个 action 的概率是 $1e-16$, 那么我们希望他增大 10 倍而不是增大1.

TRPO (Trust Region Policy Optimization)

是个老方法，但具体我也不管了

目标如下: $\max_{\theta} \mathbb E\left[\frac{\pi_{\theta}(a_t\mid s_t)}{\pi_{\theta_{old}}(a_t\mid s_t)} A_t\right]\\ \ \\ \text{subject to } \mathbb E\left[\text{KL}\left[\pi_{\theta_{old}}(\cdot\mid s_t), \pi_{\theta}(\cdot\mid s_t)\right]\right] \leq \delta$ 这样的目标就基本上是所有 RL 方法的大方向了。

至于 KL 散度如何计算：比如对于 LLM case, 对每个 token 我们知道整个 $p(a_t\mid s_t)$, 所以可以直接计算。但是对于 continuous action space, 可能需要一些近似方法 (Monte Carlo).

Problem: how to regularize

TRPO 原来的方法就是加上一个 KL penalty term

$L^{KL}(\theta) = \mathbb E\left[\frac{\pi_{\theta}(a_t\mid s_t)}{\pi_{\theta_{old}}(a_t\mid s_t)} A_t\right] - \beta \mathbb E\left[\text{KL}\left[\pi_{\theta_{old}}(\cdot\mid s_t), \pi_{\theta}(\cdot\mid s_t)\right]\right]$ 但是事实是，很难找到一个单一的 $\beta$ 能够一直表现的很好。

为此，PPO 提出了两种解决这个问题的办法 (实际上 PPO 是一族算法，并不是单一的算法)

Clipped Surrogate Objective

这个方法不显示使用 KL penalty, 间接的让 policy 不要变化太大。

方法是当 $\frac{\pi_{\theta}(a_t\mid s_t)}{\pi_{\theta_{old}}(a_t\mid s_t)}$ 变化太大时，就不让他继续变化。也就是对这个东西 clip 一下 $L^{CLIP}(\theta) = \mathbb E\left[\min\left(r_t(\theta) A_t, \text{clip}(r_t(\theta), 1-\epsilon, 1+\epsilon) A_t\right)\right]$ 式子有点难看，但是实际上很直观

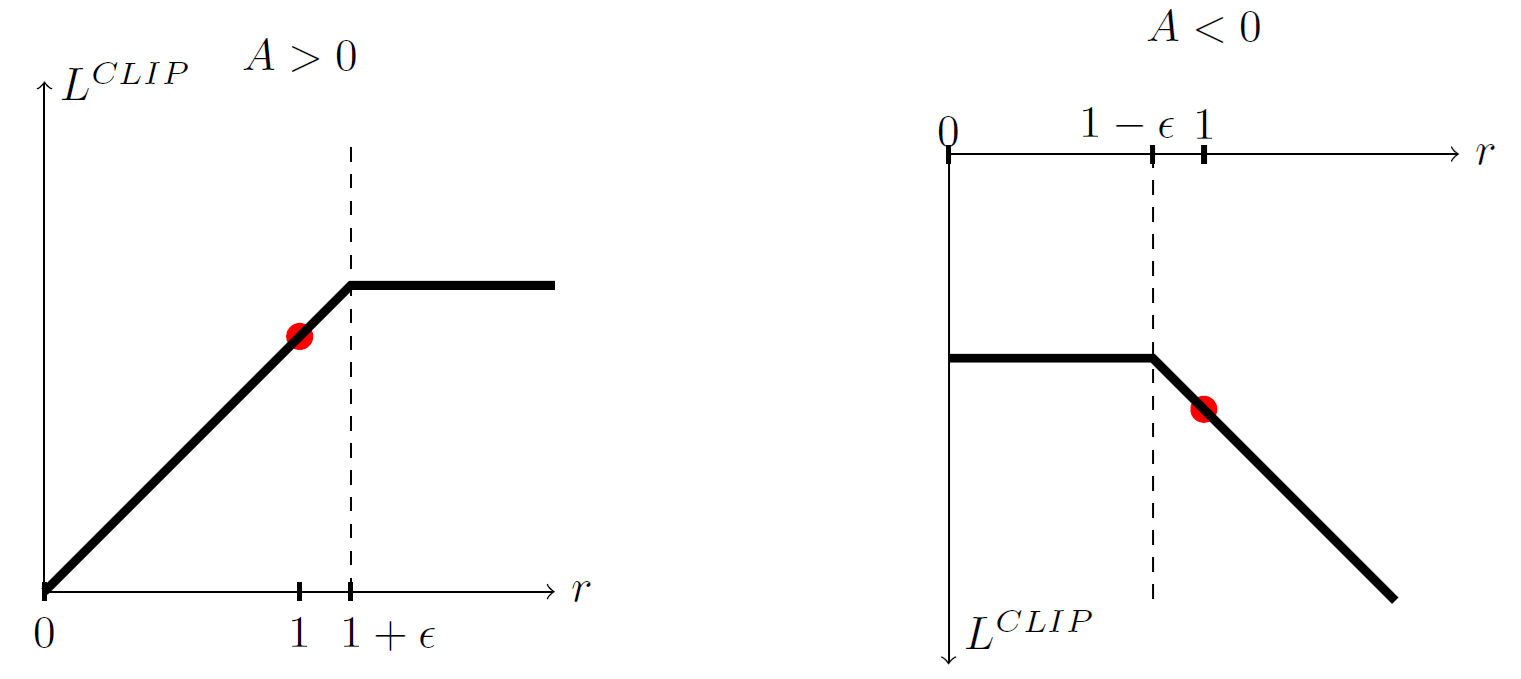
image not found

Adaptive KL Penalty Coefficient

对于有 KL penalty 的方法, 我们可以动态调整 $\beta$ 的值.

具体来说，我们设置一个阈值 $d_{target}$, 如果当前的 KL divergence 比较大 (大于 $1.5d_{target}$)，我们就增大 $\beta$, 反之减小 $\beta$.

不过经验上来说，这个方法很 sensitive, 并且不如 clip

以上就是大致的 PPO 方法。下面我们来说说在 LLM post-training 上的应用

PPO for LLM post-training

有两种情况：一种是 sparse reward (一整个答案才给一个 reward), 另一种是 dense reward (每个 token / 一段有 reward)

比如前者，我们就可以类似把一整个答案看作一个 action. 也就是，我们先 sample 一个解答，计算 reward (advantage), 计算整段话的 new/old model prob ratio，然后做 PPO update.

此外，对 LLM RL finetune 我们一般 clip + KL penalty 一起用

SQA-042

[Paper] Proximal Policy Optimization Algorithms