SQA-026
[Paper] Analyzing and Improving the Training Dynamics of Diffusion Models
神作再续: EDMv2
主要把 ImageNet-512 刷爆了. 在 64x64x4 的 latent space 上做的.
一句话概况就是, 在优化层面做了很多, 比如关注 activation 和 weight 的 magnitude 能好巨多.
从 ADM 的架构开始改的, formulation 从 EDM 的初始化. 63 步 EDM sampler.
总体来看训练 epoch 挺多的, 但是很小的模型就能刷爆大模型. batch size 用的 2048.
Tricks
Loss weighting
虽然 EDM 的 loss weighting 让初始化的时候 loss 均衡, 但是后面就不一定了. 所以做法是手动做一个 loss weighting, 把 loss scale 成 loss 的相反数.
具体做法 (由于 $t$ 是连续的) 可能是搞了一个可学习的一层 MLP, 学习 loss weighting. 类似 sCM.
这个涨得不多. 8.00 $\rightarrow$ 7.24
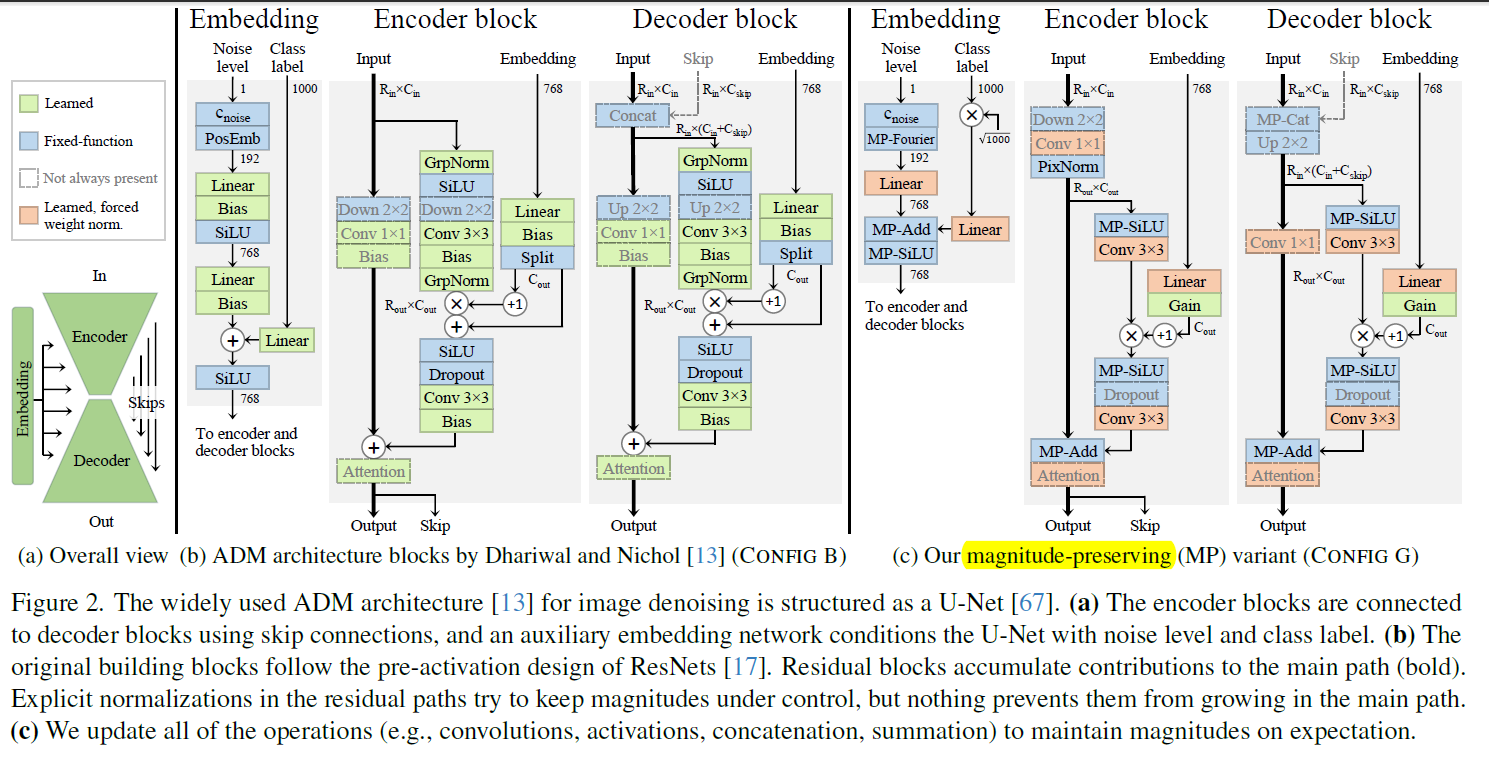
Architecture
Simplify
直接删掉了所有 bias! 发现对结果基本无害.
不过为了保持表达力, 还是在输入的图片的时候 concat 了一个全 1 的 channel.
把所有参数初始化全改成 Kaiming 初始化, embedding 改成 Fourier.
把所有的 GN 的可学习参数都去掉了, 所以只有 normalize 的效果.
Attention
发现 qkv 的大小越训越大. 于是改成使用 cosine attention, 也就是算出 qkv 之后直接 normalize.
现在经过一通简化, 7.24 $\rightarrow$ 6.96. (Config C)
Activation magnitude
发现 activation 越训越大. 解释: ADM 有很多 residual connection, 缺乏 normalization.
但是直接加很多 norm 会有害, 产生 artifacts (GAN 工作研究过).
所以选择让 expected norm 能被控制. 做法是, 比如在点乘的时候 $v\cdot w_i$, 乘完之后直接除以 $|w_i|_2$.
并且这个是放到计算图中的 (也就是不 sg). 这个理论上等价于 weight normalization.
有了这个技术就可以把所以层重新初始化成简单的 Gaussian 了.
这个涨了很多, 6.96 $\rightarrow$ 3.75. (Config D)
Weight magnitude
还没完, 虽然刚才 activation magnitude 控制住了, 但是 weight 还是越训越大.
注意到, weight 大了相当于等效 learning rate 被 decay 了. 虽然这个有些地方是有益的, 但是作者仍然想办法解决它.
做法很暴力, 就是每个 train step 之前直接把 weight normalize 了.
注意, 梯度下降的时候仍然要采用上一个技术, 其目的是让计算图能看到你除了 weight 的 norm. 这样梯度就不会有很多 weight norm 改变的方向.
在这样的基础上, 调了一下 learning rate. 采用平方根反比的 decay. $\alpha(t)=\alpha_{ref}/\sqrt{\max(t/t_{ref}, 1)}$.
这样又能涨一点, 3.75 $\rightarrow$ 3.02. 根本部诗人 (Config E)
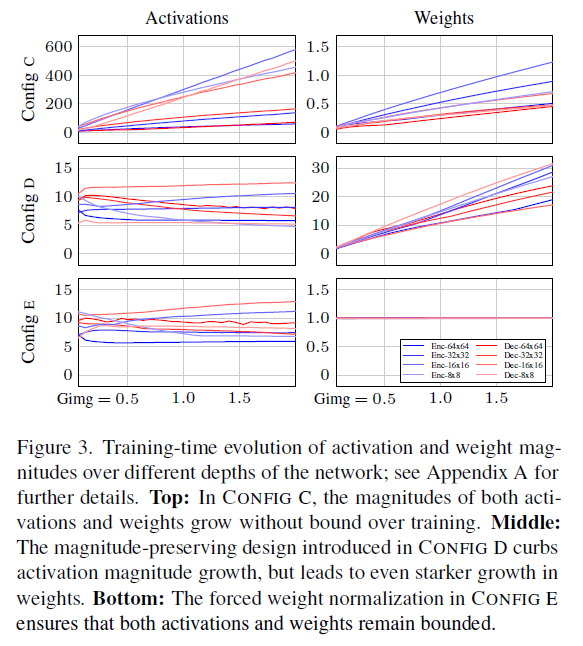
Remove GN
最后, 可以直接把 GN 扔了. 没有 norm 已经可以正常训练了, 不过发现加了一点点 pixel-norm 会有一些提升.
- pixel-norm 就是对每个 pixel, 也就是 $C$ 维的向量直接 normalize.
最后 3.02 $\rightarrow$ 2.71.
Magnitude-preserving fixed-functions
比如 silu 对于 $\mathcal N(0, 1)$ 会有一个 scale. 把这个也解决了.
还有 Fourier embedding 乘 $\sqrt 2$
对于 join paths, 手动调了 weight. 最后用的 0.3. 不唐
对于 concat, 虽然已经是 MP 的, 但是它们对 concat 后的影响正比于 channel 数. 反正说也做了一个 scale, 让总的 magnitude 期望不变但是让两部分的贡献均等.
Gain layer
有些地方还是需要 scale activation 的. 于是有一个 Gain layer: 也就是乘一个 learnable 标量. 初始化为 0.
这个 Gain layer 放在网络最最后一层. 同样, 对每一层接受 condition 进去的地方也加了 Gain layer. 也就是说, 一开始网络接受的 condition 为 0, 并且输出也为 0.
最后发现这样就可以把 dropout 给扔了!! 弱的
达成 FID 2.56. 像人
Post-hoc EMA
本文的另一大亮点, 就是允许 inference 的时候调 EMA.
不过代价是要存很多 checkpoint (基本要 16 个). 因为不需要存 adam 里面的状态, 但是每个地方要存两个不同的 EMA 参数. 结果也是近似的, 但是误差可以忽略. 感兴趣的话可以看.
Post-hoc EMA
先来确认一下 formulation. 这里我们只考虑特定的 ema schedule (为了方便计算). $\gamma$ 控制了 ema 的大小: $$ \hat\theta_{\gamma}(t) = \frac{\gamma+1}{t^{\gamma+1}} \int_0^t \tau^{\gamma}\theta(\tau) d\tau $$ 等价的 EMA 更新是: $$ \hat\theta_{\gamma}(t) = \beta_{\gamma} \hat\theta_{\gamma}(t-1) + (1-\beta_{\gamma})\theta(t) $$ 其中 $\beta_{\gamma}=(1-1/t)^{\gamma+1}$ 之后为了直观, 我们会用 relative std (也就是 width of peak value relative to training time) $\sigma_{rel}=(\gamma+1)^{1/2}(\gamma+2)^{-1}(\gamma+3)^{-1/2}$ 来指代. 比如我们说 EMA length 10% 就是指 $\sigma_{rel}=0.1, \gamma\approx 6.94$. 回到方法. 我们的做法是, 维护对 $\sigma_{rel}$ 为 0.05 和 0.1 的 EMA 参数, 然后存 checkpoint. 训练后求出这些玩意的 least squares (也就是对它们线性组合看最接近的).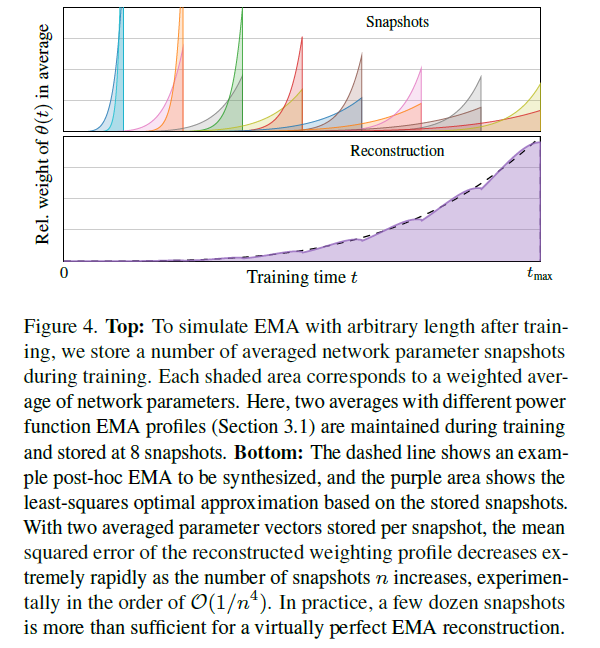
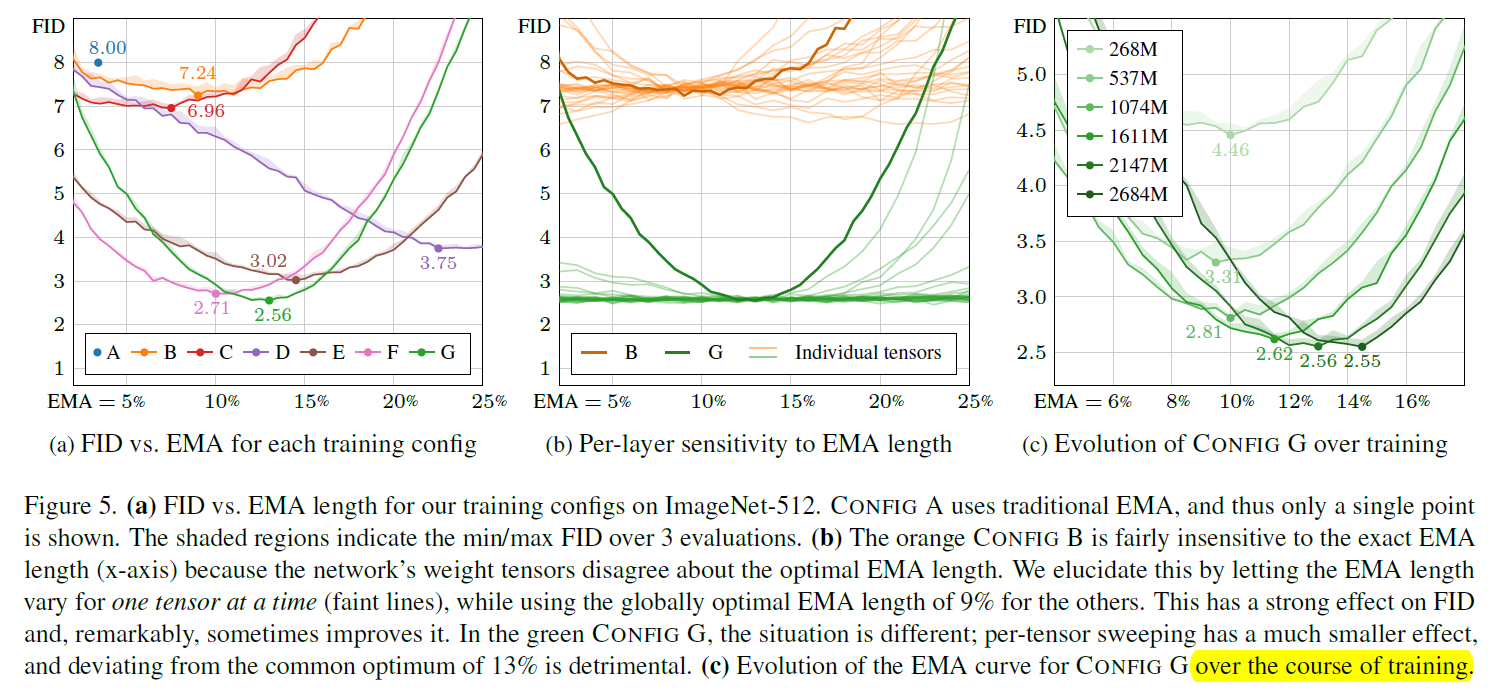
这里利用这个技术做了很多关于 ema 的 ablation. 总体看来:
- config A-G 越改对 ema 越敏感
- 如果控制只动某一层的 ema, 原来甚至能涨点, 但是现在饱和了. 活
- 训得越多, 需要的 ema 越多 (也就是 $\sigma$ 越大, 或者平均的越多)
- 模型能力越强, 需要的 ema 越弱
- 当变大 learning rate 的时候, ema length 越小. (合理的) 基本是 $\sigma_{ref}\propto 1/(\alpha_{ref}^2t_{ref})$.
Results and albations
最后对 M 以上的模型还是带了 0.1 的 dropout.
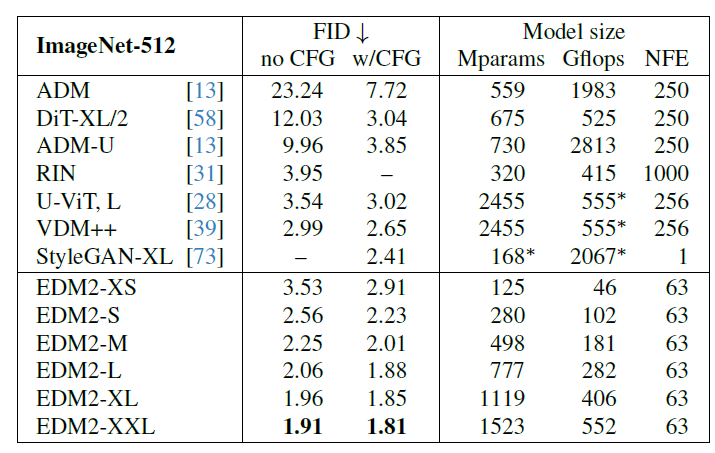
很牛, 不需要 guidance 都能用最小的模型爆锤 (虽然我猜基本 overfit to FID).
这里发现, 做 cfg 的时候, 只需要用最小的模型做 unconditional 的就行了. 这可以变快很多.
guidance scale 关于 ema 的影响很大. 唐
在 ImageNet-64 pixel 上也刷了一下, 基本吊打