简单来说, 这篇文章的方法就是在 continuous token 上做 AR 生成. 还是在 JAX 上写的.

之前大家用 transformer decoder-based model 都用 VQ-VAE 来 quantize, 然后用 categorical 预测做 AR. 现在我们直接在 $\beta$-VAE 的 latent space 上做 soft-token 的生成, 使用 Gaussian Mixture Model.

文中提到这个模型能在性能和 cost 上都超过 VQGAN.

Method

首先他们自己训了一个 $\beta$-VAE. 其中使用了 perceptual loss 和 GAN loss 来做 reconstruction.

对于 VQ-VAE 中的 look-up table, 我们直接使用一个 linear projection 来把 latent space 打到 hidden dim 上.

对于 transformer decoder 的输出, 我们让他作为 GMM 的参数 (一共 $2kd+k$ 个). 注意每个 Gaussian 的协方差矩阵假设是对角的 (也就是每个 channel 独立)

其中对于 mixture prob $\pi$, 使用 softmax 来做归一化. 对于预测的方差, 使用 softplus $\ln(1 + e^{x})$ 来保证是正的.

Training

训练的时候, 我们直接用 MLE, 也就是最大化 latent data 在预测得到的 GMM 上的概率.

GIVT-Causal: 我们一个一个 token 生成. 训练的时候加 causal mask. 对于 class label 我们对于输入序列的前面加上一个 learnable class token.

GIVT-MaskGIT: 参考工作 MaskGIT. 也就是生成的时候每次随机选一些 token 生成 (会按 likelihood 排序生成). 唯一的问题是如何选取 mask token, 作者采用下面的方法: 对于 data masked 掉的地方, 换成0然后直接过 linear embedding + transformer decoder. 此外, 还把 feature 维度 $d$ 分成两半, 一半使用 learned [MASK] or [UNMASK] token, 另一半维度减半最后 concat 起来. 略唐

Trick: Adapter (NF)

作者说这个方法可以把 VAE 和 transformer decoder 一起训, 但留给 future work. cjdl

然后还做了一个 trick, 就是 VAE latent space 后面接一个小 flow (叫做 adapter), 打到一个新的等大的 space 上做 transformer decoder.

这个 NF 使用了 VP coupling layer. 说它很小, 不足 cost 的 0.1%. 勉强能忍, 不过挺深刻的.

然后最后还是只用一个 MLE loss 来一起训这两个玩意.

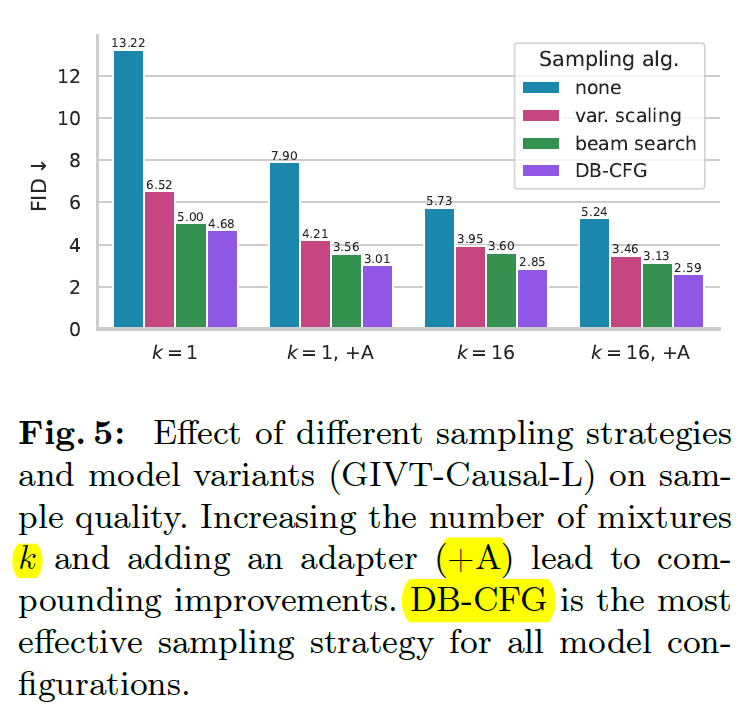
Sampling tricks

Variance Scaling: 把预测 Gaussian 的方差 scale 一下 (通常 0.8-1.0 倍). 这个好不少.
Beam Search: 字面意思.
Nucleus Sampling: 这个比较复杂, 首先对于 Mix prob $\pi$, 降序排列后累加直到比如 0.8, 然后对后面小概率的 Gaussian 直接丢掉. 然后对于每个 single Gaussian, 对每个 channel 上采样进行 clip, 也就是不要偏离平均太多倍的方差. 总之效果是把尾部分布去掉. 但文中说这个效果和 Variance Scaling 差不多, 所以弃用了.

Distribution-based CFG

似乎这个是一个很有用的 trick.

我们希望在

\[p_{CFG}(z|c) \propto p(z|c)^{1+w}p(z|\emptyset)^{w}\]

中采样. 训练的时候还是正常的 label drop 训练, 这样我们就能得到 conditional 和 unconditional 的分布. 但是如何在一个新的分布中采样呢?

使用 rejection sampling: 从一个 proposal distribution $p’$ 中采样, 然后因为我们能 track unnormalized density, 所以我们可以通过一个参数 $K$ 来 reject (未归一化的概率比例超过 $K$ 就拒绝).

但是注意这里数据是非常高维的, 所以 $p’$ 至关重要.

文中说直接使用 $\mathcal N(\mu_c, 2\sigma_c)$ 来作为 proposal distribution. 这个说是通常来说 $\sigma_{\emptyset}$ 比 $\sigma_c$ 大. 没觉得多有道理…

实测结果一般生成 1000 个 sample 就差不多能找到一个不错的. (如果没有不错的, 就重新生成 1000 个). 注意这里我们是不需要 network pass 的 (cfg 的两倍), 只需要对着输出狂日, 所以还行.

Experiments

直接在 ImageNet 256 & 512 上日.

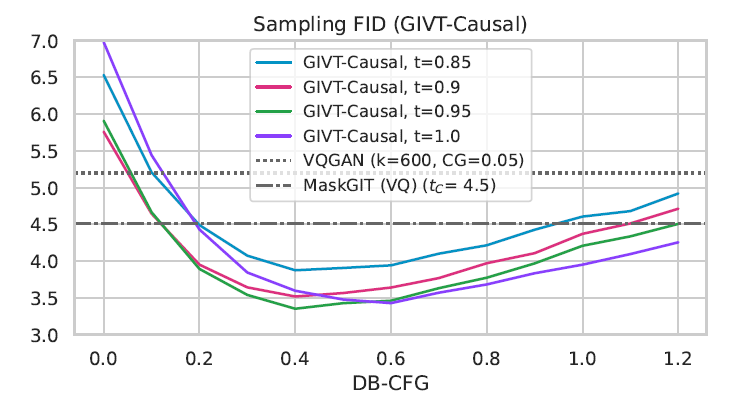
image not found

这里的 $t$ 指的就是 variance scaling (因为相当于温度).

VAE 对不同 resolution 用的同一个. token dim 为 16.