Summary: 在 Language modeling 领域, Mamba 是在 efficiency-quality trade-off 边界上介于 RNN / LSTM 和 Transformer 中间的产物. Mamba 保证了 inference 复杂度 linear scaling with sequence length. 无非还是维护一个 hidden state $h$, 但相比 RNN-based model 用了一个不同的视角, hidden state 的演化遵循不同的 parameterization.

State Space Model (SSM)

首先，我们把 hidden space, input sequence, output sequence 当作一个连续函数 $h(t),x(t),y(t)$. 注意这里 $x,y$ 是 scalar, $h$ 是一个 vector (一般情形下，每个 input channel 都有一个 hidden state vector). 定义演化方程为 \(\dfrac{dh(t)}{dt}=Ah(t)+Bx(t),\quad y(t)=Ch(t)+Dx(t).\) 对于离散的输入, 可以 discretize: $t\to t+\Delta$ 时, 定义 \(\bar A=\exp\{\Delta \cdot A\},\quad \bar B=A^{-1} (\exp\{\Delta\cdot A\}-I)B,\) 并直接从 $h(t)$ 得到 $h(t+\Delta)$.

SSM 是一个远古的 concept, 表达能力显然太弱. 事实上 $y$ 是 $x$ 的一个 convolution: \(y=x\star \bar K,\quad \bar K=[C\bar B,C\bar A\bar B,C\bar A^2\bar B,\cdots].\)

Mamba: “Selective” SSM

如果我们把 $A,B,C,D$ 甚至 $\Delta$ 变的 depend on $x$, 就能比传统的 recurrent model 有更强的表达力。在原论文中，$B,C,\Delta$ 是关于 $x$ 的网络, $D$ 强制设为 $0$, $A$ 是一个固定的矩阵，叫做 HiPPO. \(A_{ij}=\begin{cases}\sqrt{(2i+1)(2j+1)},&i<j\\i+1,&i=j\\0,&i>j\end{cases},\quad 0\le i,j<n.\) 貌似有数学上的深意，其实看，可以参考 原论文.

Mathematically, it does so by tracking the coefficients of a Legendre polynomial which allows it to approximate all of the previous history. – Exploring Language Models

$B,C,\Delta$ 是关于 $x$ 的 linear network ($\Delta>0$ 用一层 $\texttt{softplus}(x)=\log(1+\exp(x))$ 保证). 直觉上：$B$ 代表输入如何影响 hidden state; $C$ 代表 hidden state 如何影响输出; $\Delta$ 是有深意的部分, $\Delta$ 越大, 这个数据对 memory 的影响越大.

Comment: $\Delta=\Delta(x)$ 可能是其区别于 RNN / LSTM 的地方. 显然 gated recurrent network 是 Mamba 的一种特殊情况.

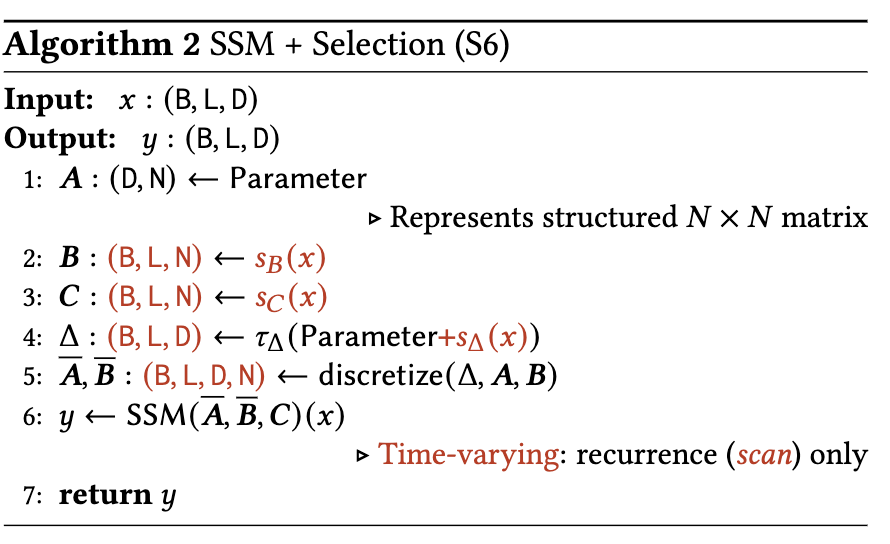
整体的架构如下图. 注意每个 input channel 都有自己的 hidden state, $B,C,\Delta$. Selection Mechanism 就是上图的 Algorithm 2.

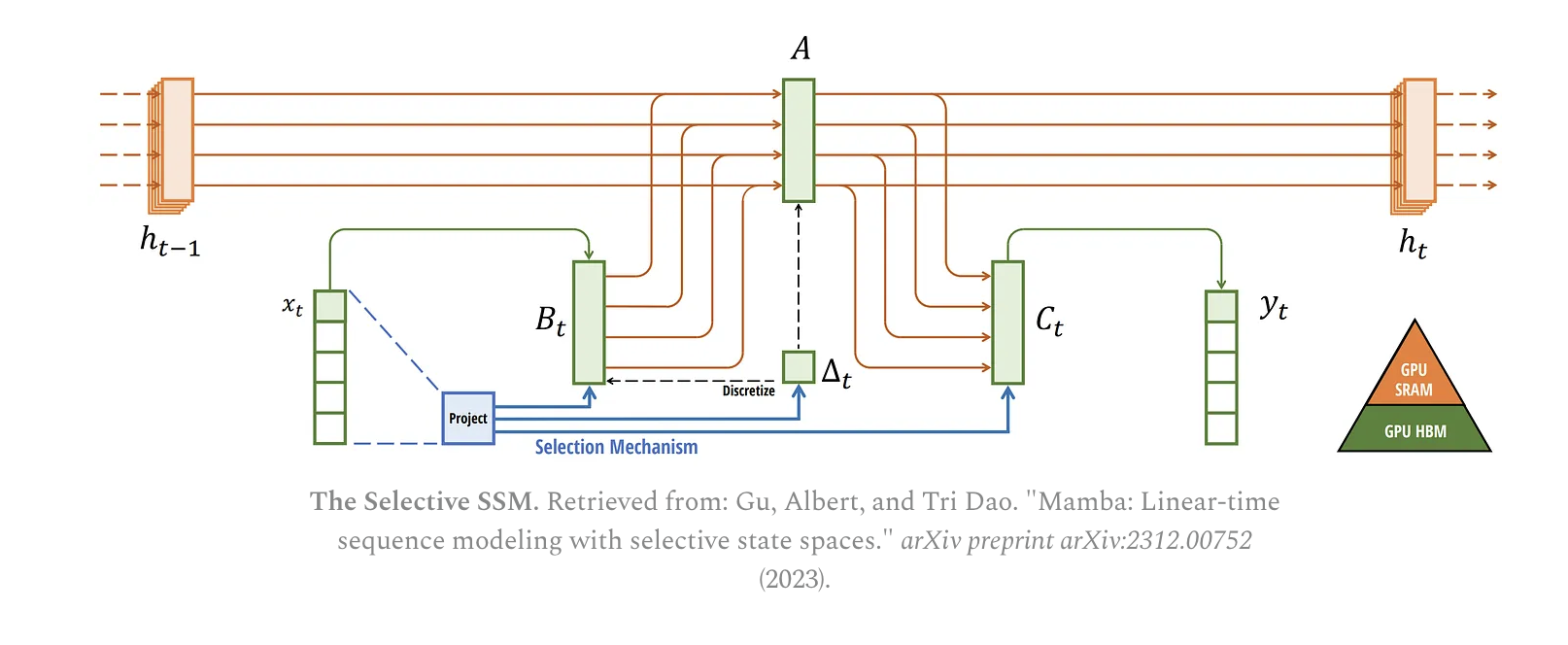
在最后的 Mamba model 中，在 SSM 外面还做了一些 skip connection, convolution, feed forward 之类, 如下图.

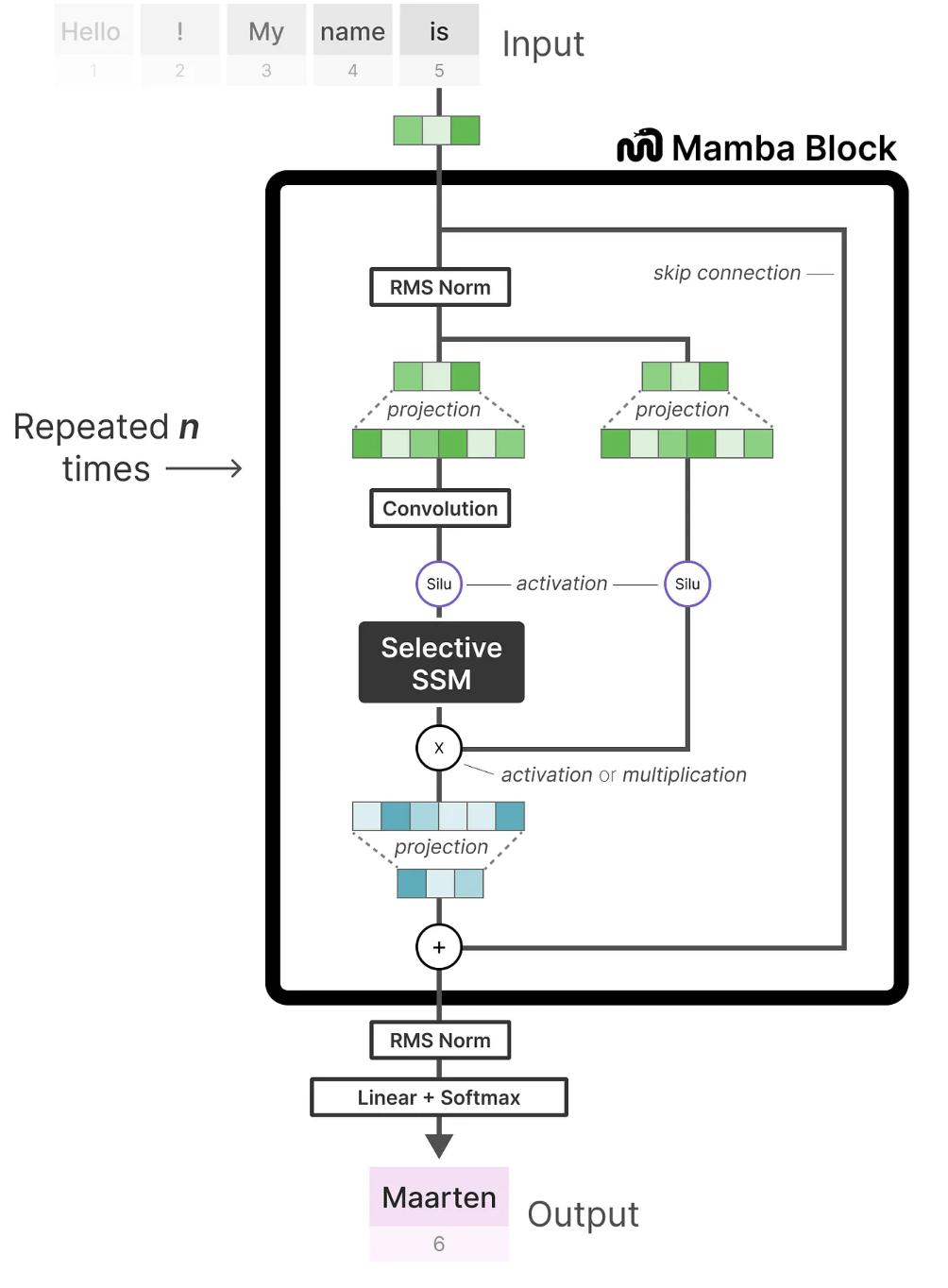
Experiments

在 GPT 2 时代, 在一些 NLP task 上达到了同模型规模 (~3B) 的 SOTA, 并且达到了 ~6B Transformer 的水平.