JZC-012

tldr: 把MoE结构运用在ViT里面

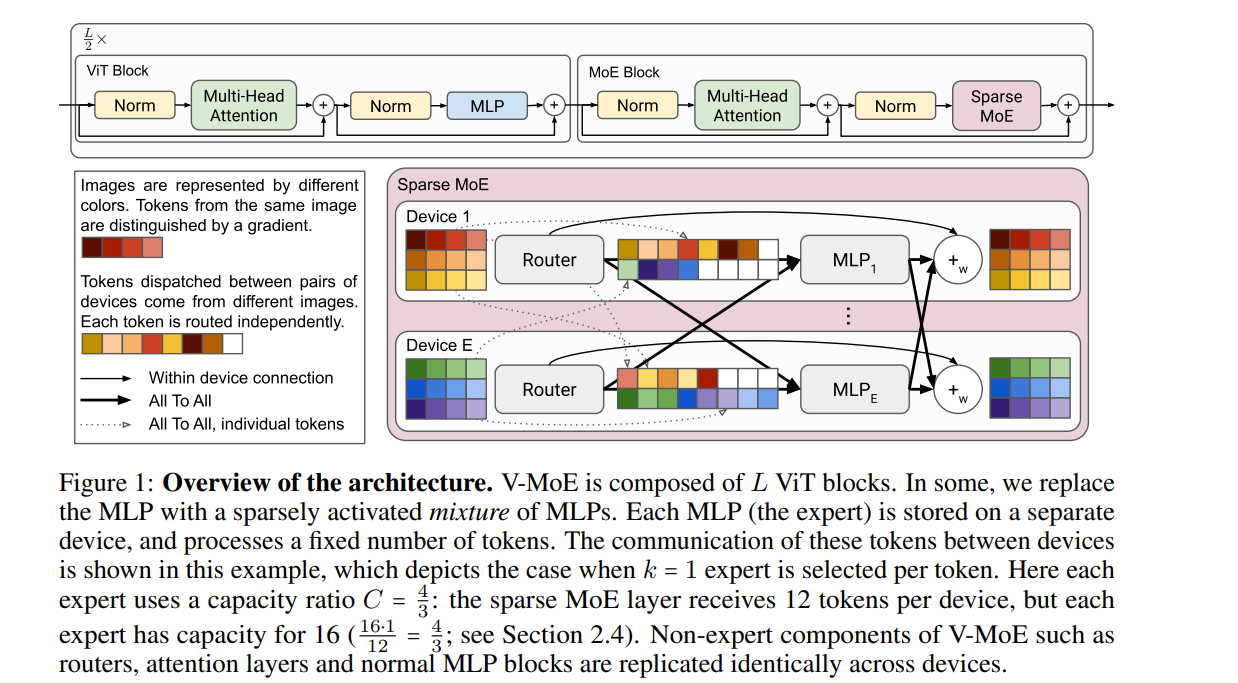
引入参数capacity ratio $C$, 表示专家的负荷程度，然后每个专家可以接受的最多token为$B_e = \text{round}(kNPC/E)$, 其中$N$是batch里面图片数，$P$是单张图片patch(token)数，$E$是专家数，$k$是每个token选择的专家个数，超过负荷限制的token将被扔掉。有意思的事情是我们可以选择$C<1$使得focus on 更有用的token,于是作者提出了Batch Prioritized Routing. 简单来说最原始的是一个一个token来选择expert, 但现在先让所有token获得一个分数，然后由分数从高到底依次向想要的expert投递志愿。

实验结果表明不同专家确实学到了不同的东西，这张图代表不同专家在不同类别的图上的weight分布。

另一件值得一提的事情是为了避免expert collapse, 作者引入了两个辅助的loss: importance loss 和 load loss.

\[Imp_i(X) := \sum_{x\in X} \text{softmax}(Wx)_i\]

直观上，$Imp_i$表示第$i$个专家对于输入$X$的重要性，然后我们可以定义importance loss: \(\mathcal{L}_{\text{imp}} := \frac{std_i(Imp)}{mean_i(Imp)}\) 但是只有importance loss,由于我们是top-k,还是会导致一些专家被忽略，所以作者引入了load loss. 注意到我们在选择专家的时候，实际上会对原始的score加上一个很小的noise，为了提高鲁棒性。而load loss从这个noise的角度提供了一个soft version的专家被选的概率，我们如下定义$load_i$表示第$i$个专家的负荷程度:

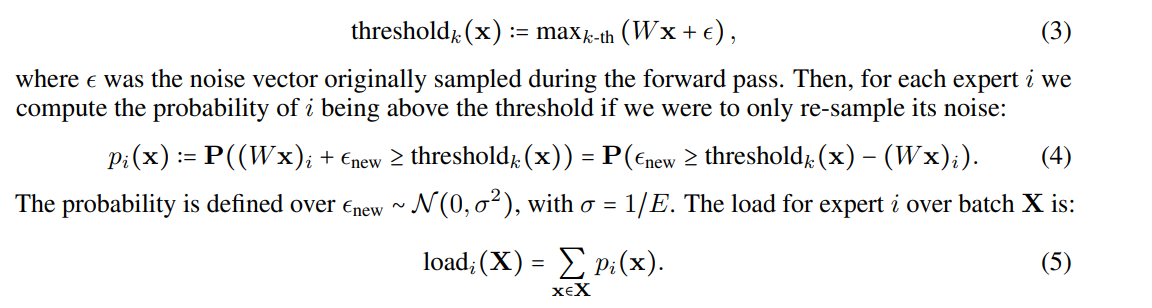
于是我们可以定义load loss:

\[\mathcal{L}_{\text{load}} := \frac{std_i(Load)}{mean_i(Load)}\]

实际运用中，我们取$\mathcal{L}{\text{imp}} + \mathcal{L}{\text{load}}$作为最终的辅助loss,并且乘上权重$\lambda$.作者用了$0.01$(实际上是0.005,因为原文是$1/2\mathcal{L}{\text{imp}} + 1/2\mathcal{L}{\text{load}}$),但文中说这个参数并不敏感。