模型微调的有名作品，tldr就是把原来的weight matrix($W$)加上一个低秩矩阵($\Delta W = BA$), 其中$W\in \mathbb{R}^{d_{in}\times d_{out}}$, $B\in \mathbb{R}^{d_{in}\times r}$, $A\in \mathbb{R}^{r\times d_{out}}$, $r$是低秩矩阵的rank，这样可以减少参数量，加速训练，同时保持模型性能。

有几个有趣的点:

  1. 我们应该LoRA哪些参数? image

作者发现，LoRA尽可能多的矩阵，用较小的$r$，效果比用较大的$r$调整一部分参数要好。

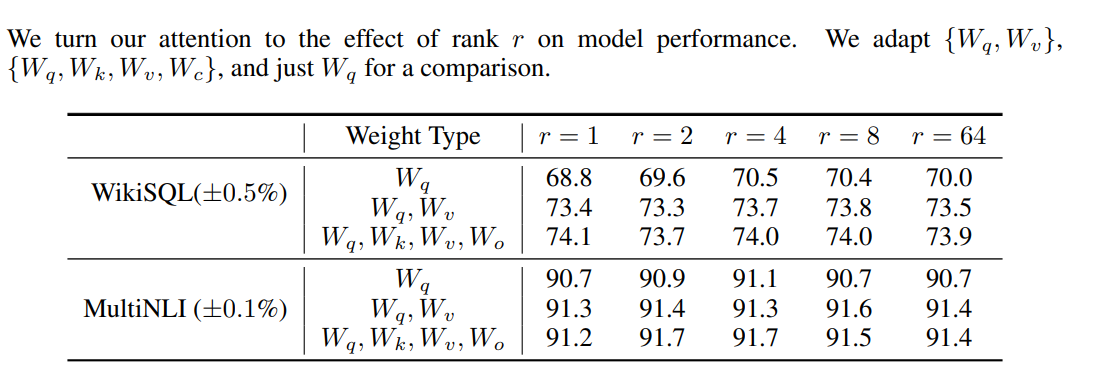
  1. $r$的选择 image

(貌似作者笔误把一个Wo写成了Wc) 作者发现，非常小的$r$就能达到很好的效果（例如$r=4,8$）。实验是在GPT-3-175B上做的，所以$r$实际上极其小。

  1. $\Delta W$学到了什么（感觉很有意思）

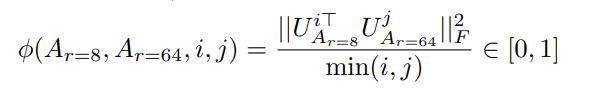
image

首先，作者对$r=8$和$r=64$的$A$矩阵的奇异值分解的右奇异空间进行距离测算，发现top-1奇异向量相似度超过0.5,并且子空间也很接近，说明他们共同学到了一些feature.

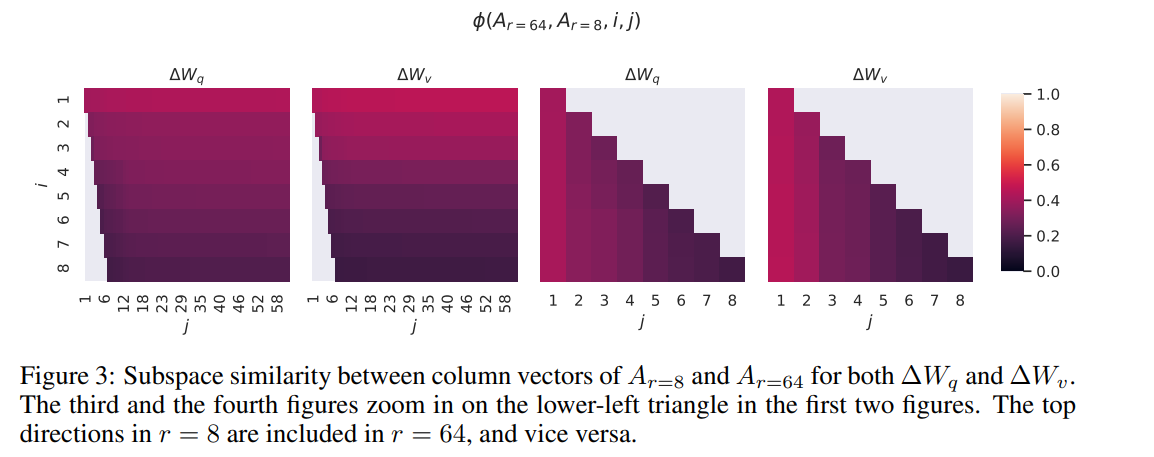
image

另外，作者观察到$W_q$似乎比$W_v$具有更高的intrinsic rank.

image

最后，这个很有意思的表格展现了$\Delta W$学到的特征(右奇异值)确实是base model忽略的，并且进行了超过20倍(6.91/0.32)的加强。这里$|W|_F$是$W$的Frobenius范数, 直观表示这个模型对特征的放大程度，也是所有奇异值的平方和的开方。非常符合直觉。