Normalizing Flow, 堂堂复活！

使用强大的 transformer 复活了 normalizing flow 这个老东西

缺点是奇慢无比

Background

使用一系列的等秩变换 $f=f^{T-1}\circ \ldots\circ f^0$ 来把 $x=z^0$ 变换成 $z^T$. 哪边是什么不重要.

其中第 $t$ 个变换形如下面的形式

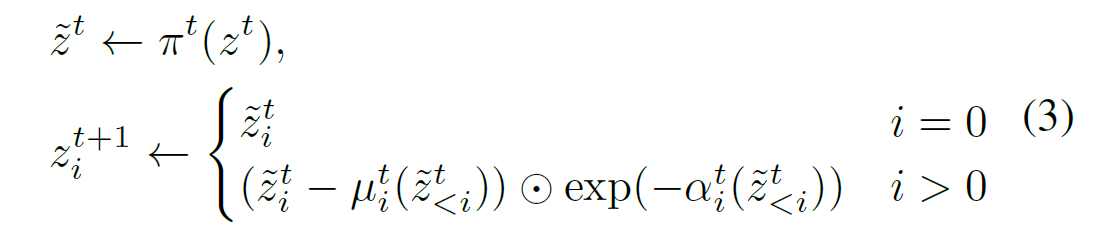
image not found

其中, $z^t$ 是该层的输入, $\pi^t$ 是一个 permutation (本文中, 只有简单的 reverse), $\mu, \alpha$ 是网络输出 (做一个 affine).

注意, 这里的下标 $i$ 指的是指第 $i$ 个 token. 这个很合理! 类似 LLM 的 autoregressive.

这样的好处就是可以有 close form 的 reverse 以及 tractable 的 Jacobian:

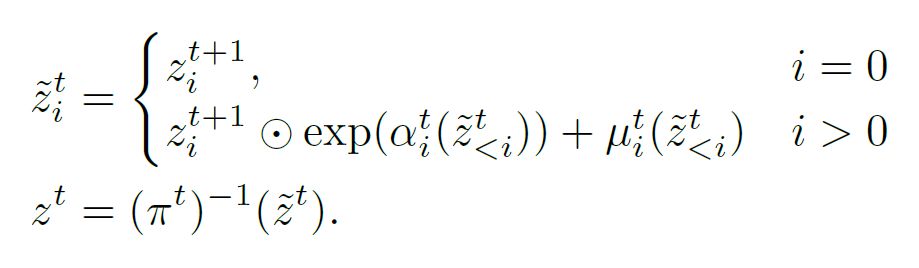
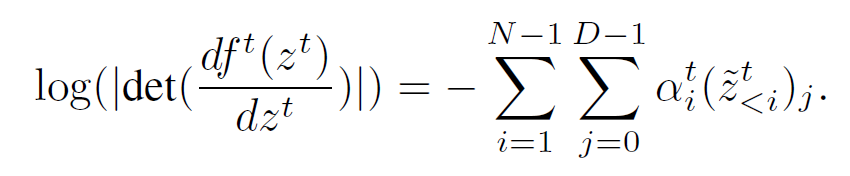
image not found

image not found

  • 这里把 coupling layer 扩展了一下, 变成一个完全 AR 的东西. 那这个就能快.

最后我们的 training objective 直接是 MLE:

\[\mathcal L = -\log p_0(f(x)) - \log(\left|\det\left(\frac{df(x)}{dx}\right)\right|)\]

这里我们把 $z^T$ 选作 Gaussian, $p_0$ 为 data

Techniques: TarFlow

首先把图片 patchify 成 token, 然后直接拍 ViT.

注意这里每个变换都是多层的 ViT.

Noise augmentation

重要的技巧: 学习的分布是加噪的. 一般加噪的等级是 0.05.

Denoising

这里我们仍然使用学出来的 model 来去噪! 由于我们现在有了概率密度, 可以获得 score function $\nabla_y \log p_{\theta}(y)$

这里 $y$ 是加噪的图片. 然后我们使用

\[x = y + \sigma^2\nabla_y \log p_{\theta}(y)\]

来去噪. 很有意思!

CFG

发现直接对每个变换拍 CFG 就很好! 不知道怎么解释, 管的吧

Unconditional Guidance

文中提出了一种新的 Guidance, 是为了 unconditional generation 设计的.

其中使用 $\mu^t(z^t_{<i};\tau)$ 来 parametrize. 这里 $\tau$ 是 attention 中的温度. $\alpha$ 同理

直觉: $\tau=1$ 应该好, 别的应该差一些, 所以对这个做一个 Guidance:

\[\tilde\mu^t(z^t_{<i};\tau) = (1+w) \mu^t(z^t_{<i};1) - w\mu^t(z^t_{<i};\tau)\]

这个挺有意思, 反正能涨点.

还提到我们对不同的 $i$ 应该使用不同的 $w$, 即有一个 schedule $w_i=\frac{i}{T-1}$. 这个其实挺合理的, 因为看到的 token 数目不一样.

Experiments

数据集: ImageNet 64 & 128, CelebA-HQ 256

使用了 1e-4 的 weight decay, drop label 0.1

总体结果和 SOTA 比差的不多, 挺牛的

CFG 用 2.0, unconditional guidance 用 $\tau=1.5, w=0.2$

关于 scaling: 在固定总层数的情况下, 8x8 比较好

Trajectory

比较神秘的是, 发现路径和 diffusion 差不多.

image not found