tl;dr: 只是改了 diffusion loss 在每个 time level (or equivalently noise level) 的 weight, 然后发现有更好的效果。并且证明了他们的 loss 等价于做 Gaussian perturbation augmentation 之后的 ELBO。

先不管 $\theta$ 网络的 parameterization, 任何 diffusion loss 都可以写作

\[\mathcal L=\mathbb E_{x\sim \mathcal D,t\sim \mathcal U(0,1),\epsilon\sim \mathcal N(0,I)}\left[ w(t)\cdot \|\epsilon_\theta(z_t,t)-\epsilon\|_2^2\right].\]

其中 $z_t=\alpha_t x+\sigma_t \epsilon$. 考虑 log-SNR $\lambda(t)=\log({\alpha_t}^2/{\sigma_t}^2)$, 它一定是关于 $t$ 的一个单调递减函数。根据简单微积分，$\mathcal L$ 也可以写成随机取 $\lambda$ 的形式，

\[\mathcal L=\int_{\lambda_{\min}}^{\lambda_{\max}} W(\lambda)d\lambda\cdot \mathbb E_{x,\epsilon} \|\epsilon_\theta(z_\lambda,\lambda)-\epsilon\|_2^2.\]

精彩操作 I

现在我们考虑 ELBO

\[\mathcal J_t := D_{\text{KL}}(q(z_{t\sim 1}\mid x)\|p(z_{t\sim 1})).\]

这里只考虑 time step $\ge t$, 相当于对 dataset 做了一个 perturbation (augmentation) $x\to \alpha_t x + \sigma_t \epsilon$ 之后的 ELBO. (这里 $t\sim 1$ 实际上是一个连续的东西，但其实管 rigorous math) 事实上可以证明

\[\mathcal J_t=C_1\cdot \int_{\lambda(t)}^{\lambda_{\max}} d\lambda\cdot E_{x,\epsilon} \|\epsilon_\theta(z_\lambda,\lambda)-\epsilon\|_2^2 + C_2.\]

所以，假如 $W(\lambda)$ 关于 $\lambda$ 非严格单调递减，或者 $w(t)$ 关于 $t$ 非严格单调递增，$\mathcal L$ 就可以写成 ELBO $\mathcal J_t$ 的某个正的线性组合。

精彩操作 II

注意到在训练的时候可以 importance sampling

\[\mathcal L=\mathbb E_{\lambda\sim p(\lambda)}\left[ \dfrac{W(\lambda)}{p(\lambda)}d\lambda\cdot \mathbb E_{x,\epsilon} \|\epsilon_\theta(z_\lambda,\lambda)-\epsilon\|_2^2\right].\]

为了使得方差最小化，我们需要

\[p(\lambda)\propto W(\lambda)\cdot E_{x,\epsilon} \|\epsilon_\theta(z_\lambda,\lambda)-\epsilon\|_2^2.\]

于是引入 adaptive noise schedule, 训练的时候考虑把 $\lambda\in [\lambda_{\min},\lambda_{\max}]$ 分成 100 个 bin，每个 bin 记录右边那坨的 EMA, 根据它来每次取样新的 $\lambda$.

实践上它能显著改进 EDM sampler 的 convergence speed。

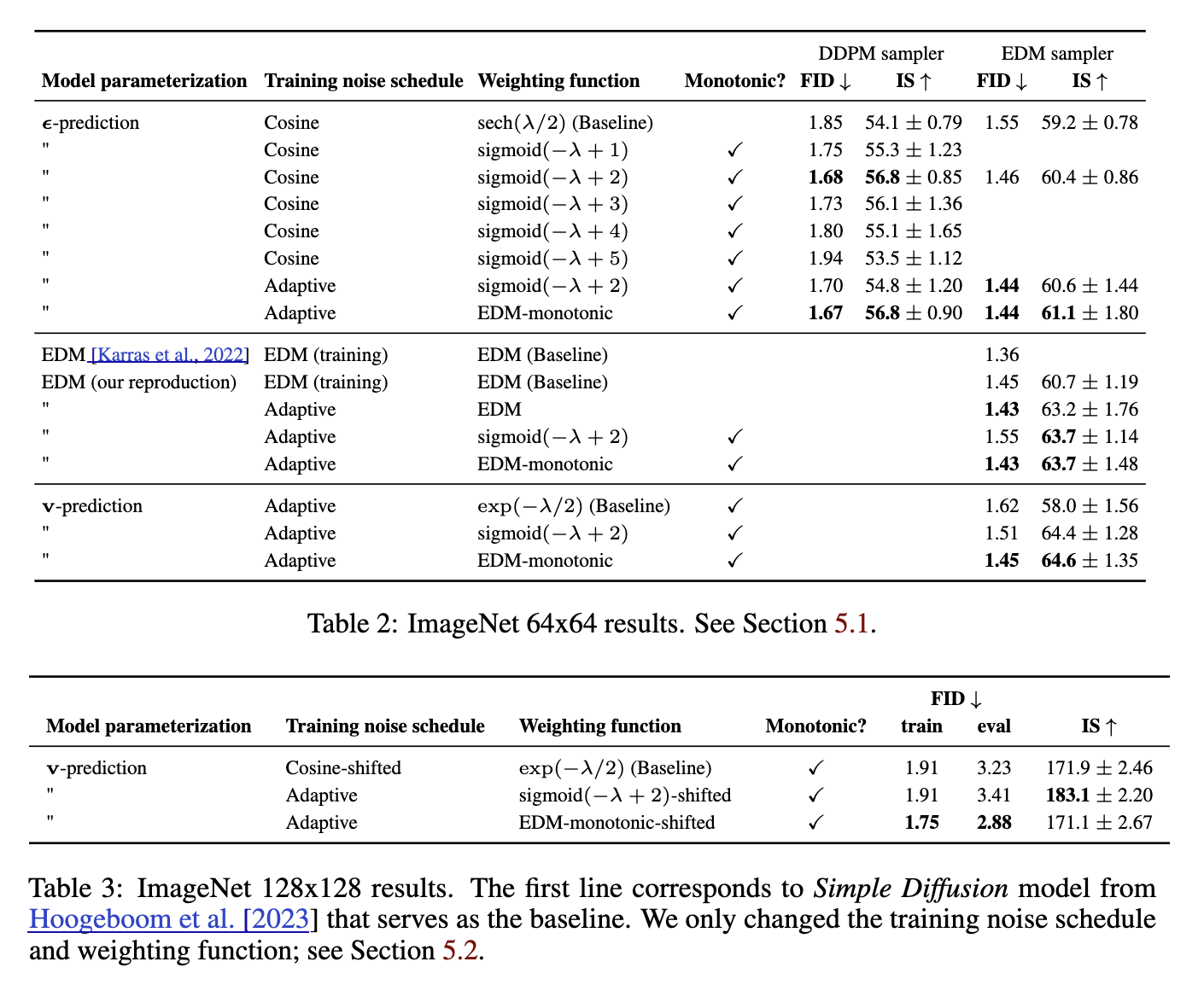
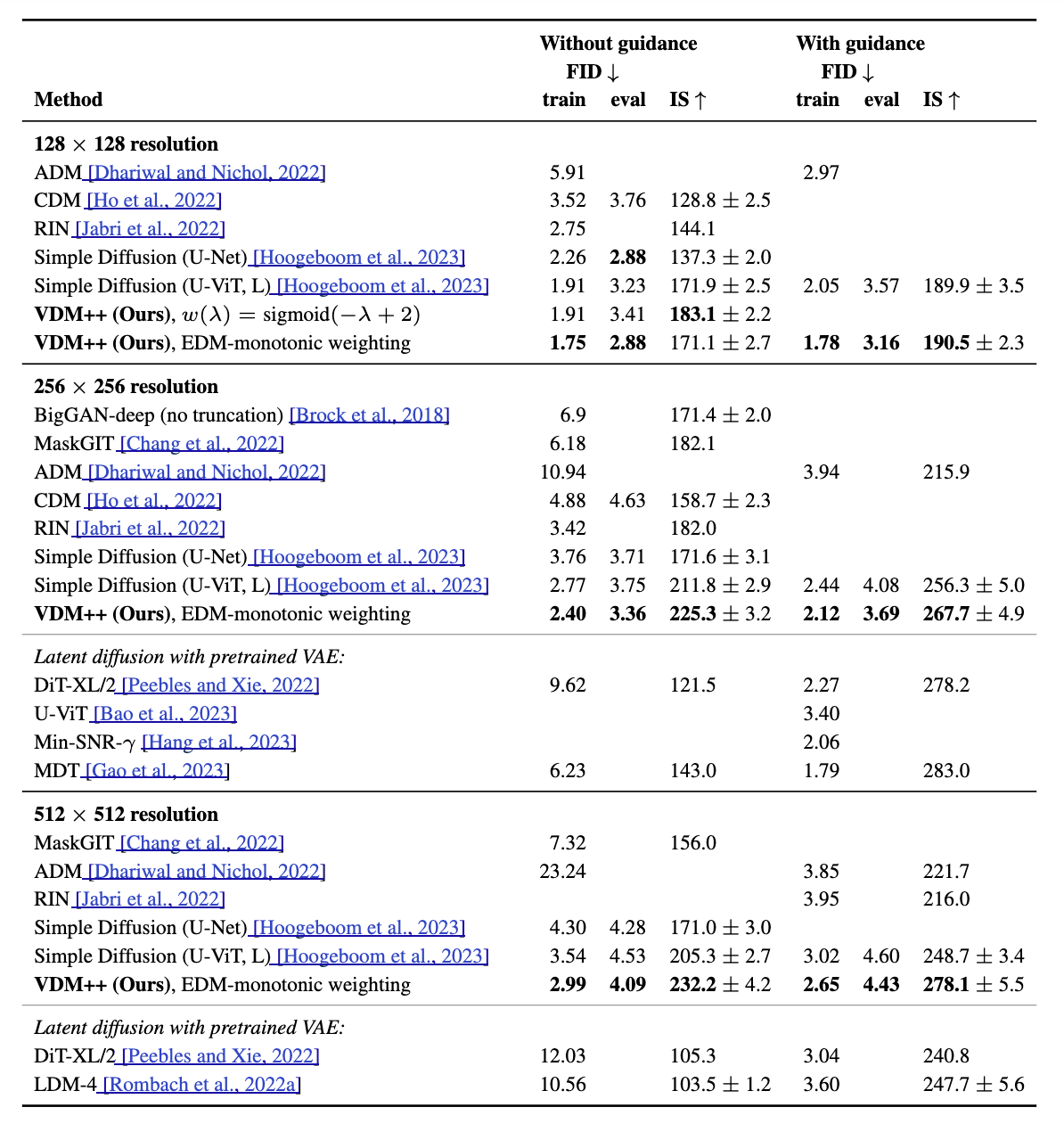
Experiments

有些 diffusion loss 对应的 $W(\lambda)$ 不是递减的，比如 EDM (which is Gaussian). 于是作者强行改成了递减：

\[W'(\lambda)\leftarrow \max_{\lambda'\ge \lambda} W(\lambda'),\]

叫做 EDM-monotonic. 还尝试了一些手搓的递减函数，加在 VDM 上，起名为 VDM++.