Motivation: ResNet 的 formulation 是 $h_{i+1}=h_i+f_{\theta_i}(h_i)$, 其中 $i$ 是 layer. 如果 layer 数量细分到无限小, 就可以变成一个 ODE:

\[\dfrac{dz(t)}{dt}=f_\theta(z(t),t),\]

其中 $z(t)$ 是 $t$ 时刻的 state。

Comment: 这篇论文相当于把一个普通的 end-to-end training 变成一个连续化的 ODE。但它和 Diffusion (ODE models) 的本质区别是，Neural ODE 还是局限在 end-to-end，而 ODE models 是在匹配每一小步。直接后果是前者的 simulation 误差会累加，Diffusion 不会；并且后者会好学很多。

Reverse-mode automatic differentiation of ODE solutions

假设我们的 objective 是 $\mathcal L(z(1))$, 概率分布 $p(z(0))$ 已知。如何求出 $d\mathcal L/d\theta$？考虑 backprop 的连续版本，我们需要 track $d\mathcal L/dz(t)=:a(t)$ (paper 中叫做 adjoint). Adjoint 需要通过 reverse ODE 求解, 方程为

\[\dfrac{da(t)}{dt}=-a(t)^T\dfrac{\partial f_\theta(z(t),t)}{\partial z}.\]

利用 $a(t)$ 可以求出

\[\dfrac{d \mathcal L}{d \theta} = -\int_{0}^1 a(t)^T\dfrac{\partial f_\theta(z(t),t)}{\partial \theta}dt.\]

注意到这里可以 memory-efficient training: 我们只需要记录 $z(1)$，通过 autograd 算出 $a(1)$ 之后用 ODE solver 同时 simulate $z,a$，而不必记录 forward process 中间层的结果。进一步地，可以通过 tune ODE solver 的 tolerant error 来 trade-off between quality and speed.

如果一个 network 存在 downsample layer，那么我们需要记录 downsample 前的 $z$ 才能计算出 $\dfrac{d \mathcal L}{d \theta}$.

Experiment: Replacing residual networks with ODEs for supervised learning

在 MNIST 上把 ResNet 替换为 ODE model，在表现几乎相同的情形下降低了空间开销 ($O(1)$ instead of $O(L)$).

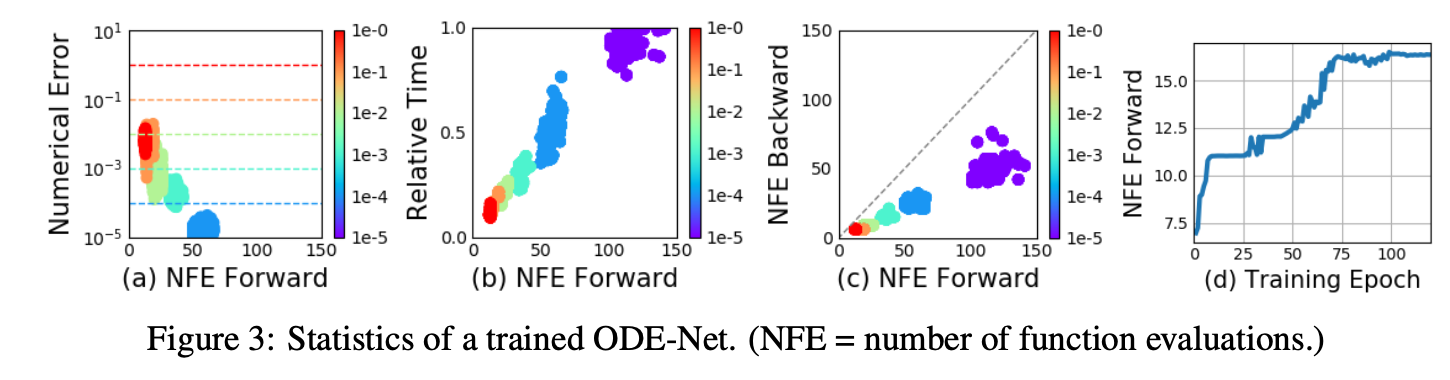
Some findings: Forward NFE 大于 Backword NFE (表明比直接按照 forward 的 discrete timestep 反过来 backward 要 efficient); 训练过程中 NFE 逐渐增加，体现 $f_\theta$ 逐渐变得复杂。

Continuous Normalizing Flows

注意到，planar flow $z_{t+1}=z_t+uh(w^Tz_t+b)$ 也可以连续化为 ODE

\[\dfrac{dz(t)}{dt}=uh(w^Tz(t)+b).\]

为了 track likelihood, 可以证明如下结论：对一个 ODE $\dfrac{dz(t)}{dt}=f(z(t),t)$, 有

\[\dfrac{\partial \log p(z(t))}{\partial t}=-\text{tr}\left(\dfrac{df}{dz(t)}\right).\]

好处：比起 $\det$, $\text{tr}$ 的计算复杂度更低。

  • continuous normalizing flows (CNF)：定义 \(f(z(t),t)=\sum_{i=1}^n \sigma_i(t)f_{\theta_i}(z),\) 其中 $\sigma$ 是可学习的 scalar, $\in (0,1)$.

实践上，CNF 比 NF 更能拟合复杂分布.

A generative latent function time-series model

还可以把 RNN 变成连续的模型: $z$ 表达的是 latent vector sequence.

\[z(0)\sim p(z(0)),\quad \{z(t_i)\}_{1\le i\le N}=\text{ODESolver}(z(0),f_\theta,\{t_i\}),\] \[x(t_i)=p_\phi(x\mid z(t_i)).\]

Scope and Limitations

  • Mini-batch: batch 中的每个 data piece 可能会让 ODE solver 走不同的 discrete time step, 从而让 simulation 的时间变长。但实践上不会 degrade 很多。
  • Reverse approximation: reverse process 需要 reconstruct 出 forward process, 这里面的误差会导致更大的训练误差。