这个方法从 FM 的基础上扩展想做一步生成. 想法是, 多加一个 condition step size $d$. 网络记作 $s_{\theta}(x_t, t, d)$.

注意这个 $s$ 类比速度, 也就是两个地方的差.

$x_0$ 是 noise, $x_1$ 是 data

Objective:

\[\mathcal L=\mathbb E_{(x_0,x_1)\sim (\mathcal N,\mathcal D),(t,d)\sim p(t,d)} \left[\|s_\theta(x_t,t,0)-(x_1-x_0)\|^2+\|s_\theta(x_t,t,2d)-s_{\text{target}}\|^2\right],\]

其中

\[s_{\text{target}}=\textbf{sg}(\dfrac{1}{2}(s_{\theta}(x_t,t,d)+s_{\theta}(x_{t+d}',t+d,d))),\]

$x_{t+d}’$ 是在 $t$ 处的预测结果 $x_t+d\cdot s_{\theta}(x_t,t,d)$. 第一项是基础的 flow matching loss, 第二项是 self-consistency loss.

Details

Train $t$ and $d$ schedule

$t\sim \mathcal U(0,1)$; 论文中 sample step 是 $128$, $d$ 取值为离散的: $d\in {\dfrac{1}{128},\dfrac{1}{64},\cdots,1}$. 这个还是唐.

最唐的是, 注意到上面 loss 中会觉得奇怪, 只有 $d=0$ 的时候有监督. 原来, 作者对 $d=1/128$ 的时候直接把 $d$ condition 选成 0. 搞的不错

更唐的是, $t$ 的选取只训 $d$ 的整数倍. 都什么年代了

训练的时候，一个 batch 分为两部分, 分别 train flow matching loss 和 self-consistency loss；两者的比例是 $(1-k):k$, $k$ 取 $0.25$. 作者 claim 在训练过程中如果出现 self-consistency loss 不稳定的情况，就要减少 $k$. 这不是废话, 多写个系数能咋地

hyperparameters

  • lr: const 1e-4
  • weight decay: 作者说 weight decay 是关键, 否则不稳定. 很奇怪. 用的 0.1
  • CFG: 这里 few step 不适用. 多练

Live Reflow

一笔带过的玩意, 还挺有意思: 把模型同时用 FM loss + Reflow loss 训练, 其中 Reflow target 每次都是自己模拟出来的.

Experiments

实验竟然直接在 CelebA-256 / ImageNet-256 的 latent 上做, 用的 DiT-B/2 架构. 牛的

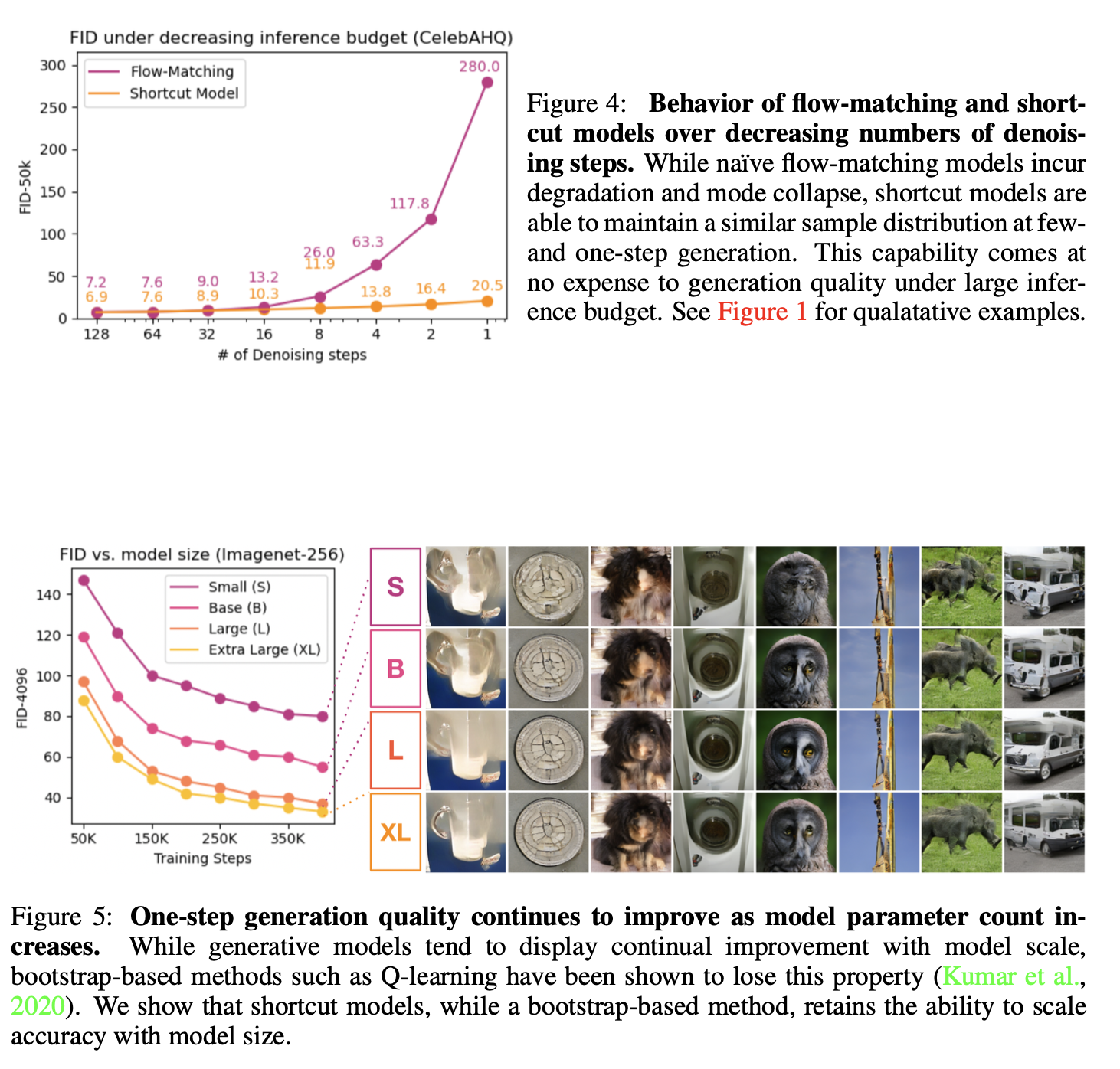
步数减少到 1 步仍然能生成较好的图片; 且观察到了某种 scaling law? One-step generation 吊打了 consistency training (CelebAHQ-256 & Imagenet-256); 但是不如 two-stage 的 progressive distillation。

作者还测了 robotics tasks 上的表现。不愧是 Sergey Levine。