Two roads diverged in a wood, and I –
I took the one less traveled by,
And that has made all the difference. - Robert Frost

提出了一个新的 optimization 的方法, 不同于 cosine schedule 等方法需要提前指定 stopping time $T$, 并且能达到更好的收敛效果。

应用到 SGD 和 AdamW 上，分别有 Schedule-free SGD 和 Schedule-free AdamW。

  • Schedule-free SGD: $x$ 是 evaluation sequence (是最终学习的参数), $y$ 是 gradient location sequence, $z$ 是 base sequence: \(y_t=(1-\beta)z_t+\beta x_t,\) \(z_{t+1}=z_t-\gamma \nabla f(y_t,\zeta_t),\) \(x_{t+1}=(1-c_{t+1})x_t+c_{t+1}z_{t+1}.\) 其中 $\zeta_t$ 是随机变量，相当于 $\nabla f$ 的一个无偏估计; $c_{t+1}=(t+1)^{-1}$.

    • 相当于对 $z$ 做 SGD, 但使用 $y$ 处的 gradient; $x$ 是前面所有 $z_t$ 的 average, $y$ 是 $x$ 和 $z$ 的一个 interpolation (实践上 $\beta=0.9$ 或 $0.98$).
    • 深意 1: 有理论保证 (Theorem 1 for $\gamma\propto 1/\sqrt{T}$; Theorem 3 for constant $\gamma$). 管
    • 深意 2: 考虑这个方法比 EMA 好在哪里，假设我们有一个 immediate large gradient $g_t$, 那么 EMA 会 exponentially 吸收这个 impact, 造成短时间内爆炸；但 schedule-free SGD 用 $x_t$ 来吸收这个变化, 就会相对平和; 另一方面, 如果直接让 $\beta=1$ (叫做 Primal averaging), 那么单步的 gradient 作用又太小了，收敛速率慢。

  • Schedule-free AdamW: 改一下 estimated gradient。下图还加了一个 warmup stage 并且改变了 $c_{t}$ 的 schedule (因为每次的 learning rate $\gamma_t$ 变了)

Experiment

下面的每根红线都是一个 cosine schedule, 黑线是 schedule-free 的, 发现完全优超。

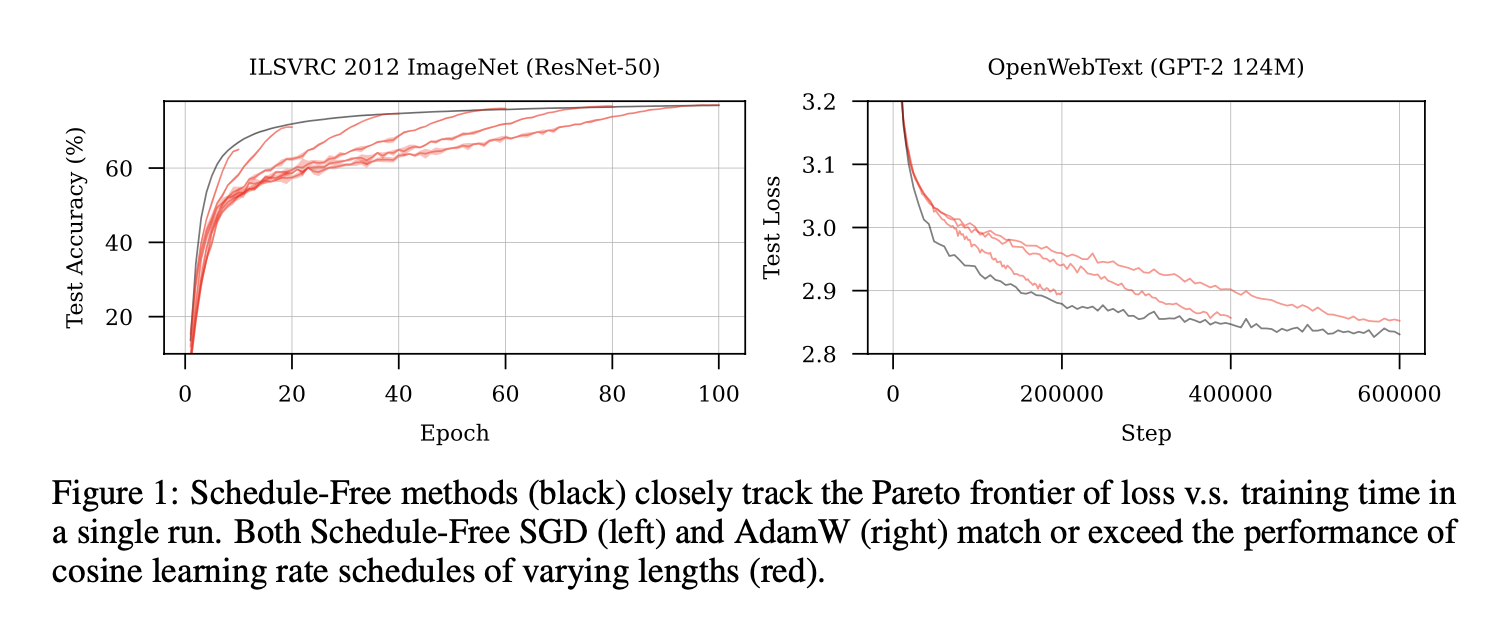
实验包括 CIFAR, Imagenet 上跑 ResNet / DenseNet, 还有一些 NLP task, $\beta=0.9$ 效果都不错 (除了一个任务不稳定，需要 $\beta=0.98$)