本文要解决的主要问题是 Consistency model 训练时间太长的问题. 提出了 Easy Consistency Tuning 方法, 有效减少了计算消耗, 还能保证生成效果, 还保证了 scaling law. 看上去很吊打

Formulation

consistency model $f(x_t, t)=x_0$ 等价于两个条件: $df/dt=0$ and $f(x_0, 0)=x_0$. (称作 consistency condition)

训练的时候使用

\[\frac{f_{\theta}(x_t)-f_{\theta}(x_r)}{t-r}\]

来近似 $df/dt$. 一般的 loss 形式是

\[\mathbb E_{x_0, \epsilon, t}w(t, r)\text d(f_{\theta}(x_t), f_{\text{sg}\theta}(x_r))\]

with $w(t, r)=1/(t-r), x_t=x_0+t\epsilon, \epsilon\sim p(\epsilon)$

其中两次 forward 的 dropout seed 要一致.

Problem

在 $N$ 大的时候, 误差会积累, 而 $N$ 小的时候不准. 这导致了很长的训练时间.

ECT: Easy Consistency Tuning

核心路径是先 pretrain 一个 diffusion model, 然后再 tune 成 consistency model.

其中取的时间步骤 $\Delta t$ 一开始很大 (比如取 $t, 0$), 最后慢慢变小, 这样就能平滑的从 DM 目标到 CM 目标. 这有道理吗。。

Pros: 即使 pretrain 一个 DM 也减少了很多 training cost

image not found

Design

Mapping function: choose of time steps

文中把 $p(r\mid t)$ 叫做 mapping function. 注意这里我们设计对用一个 $t$ 唯一确定 $r$! 这有道理吗?

实际上, 我们还 condition on epochs. 注意到我们想要让训练后期 $r$ 接近 $t$, 我们的 parametrization 如下:

\[\frac r t = 1-\frac 1 {q^a} n(t) = 1-\frac 1 {q^{[\text{iters}/d]}}n(t)\]

然后让 $n(t)=1+k\sigma(-bt)=1+\dfrac{k}{1+e^{bt}}$. 一般来说我们取 $q>1, k=8, b=1$. 然后 clamp $r\ge 0$.

  • 这样训练初期就有 $r/t=0$, 和 DM 一致.

  • 想看这是怎么设计的, 见 Appendix A

Choice of metric

作者认为 Psuedo-Huber loss 应该被看成是 $L_2$ loss 乘一个 adaptive scaling factor $w(\Delta)$, 其中 $\Delta$ 是差异.

这样就直接取 $L_2$ 然后在 weight 中讨论.

Weighting

Weighting function 很重要!

这里采用了两个 weighting: ($\Delta=f(x_t)-f(x_r)$)

\[w(t)=\bar w(t)\cdot w(\Delta)=\bar w(t)\cdot\frac 1 {\sqrt{\|\Delta\|_2^2+c^2}}\]

其中 $\bar w$ 叫做 timestep weighting, $w(\Delta)$ 叫做 adaptive weighting. (这个有深意的选取是有深意的)

Results

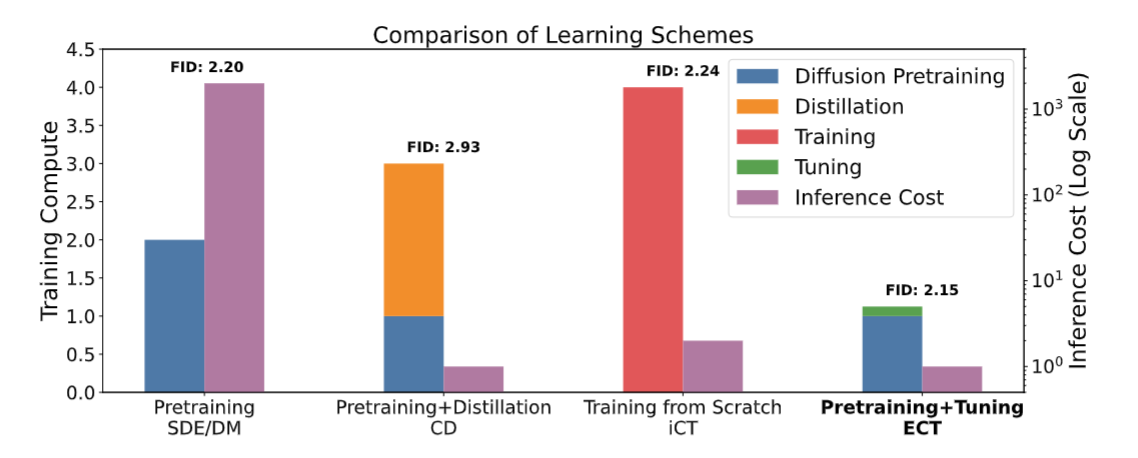
image not found

可以看到, training cost 和 Distillation 差不多, 但效果好多了!

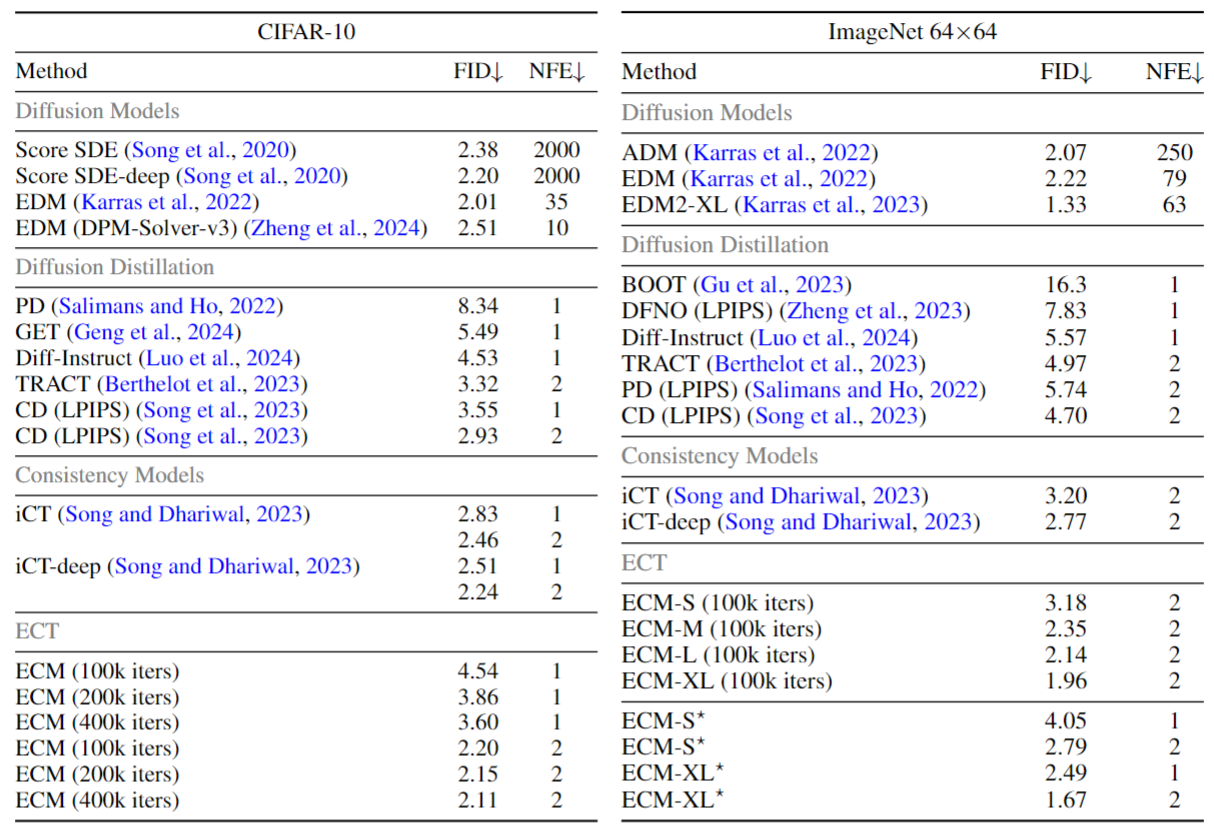
image not found

发现 2-step FID 很好, 超越了 ICM! 但是 1-step 稍微差一点, 但已经很好. 训练的消耗可以达到 ICM 的 1/3 到 1/4.

这个 Blog 中提到, 与其完全追求一步法生成, 不如把模型大小减半, 然后做两步生成. 实际上这样确实效果更好!

Scaling laws

在同一个模型做不同步数的 fine-tune.

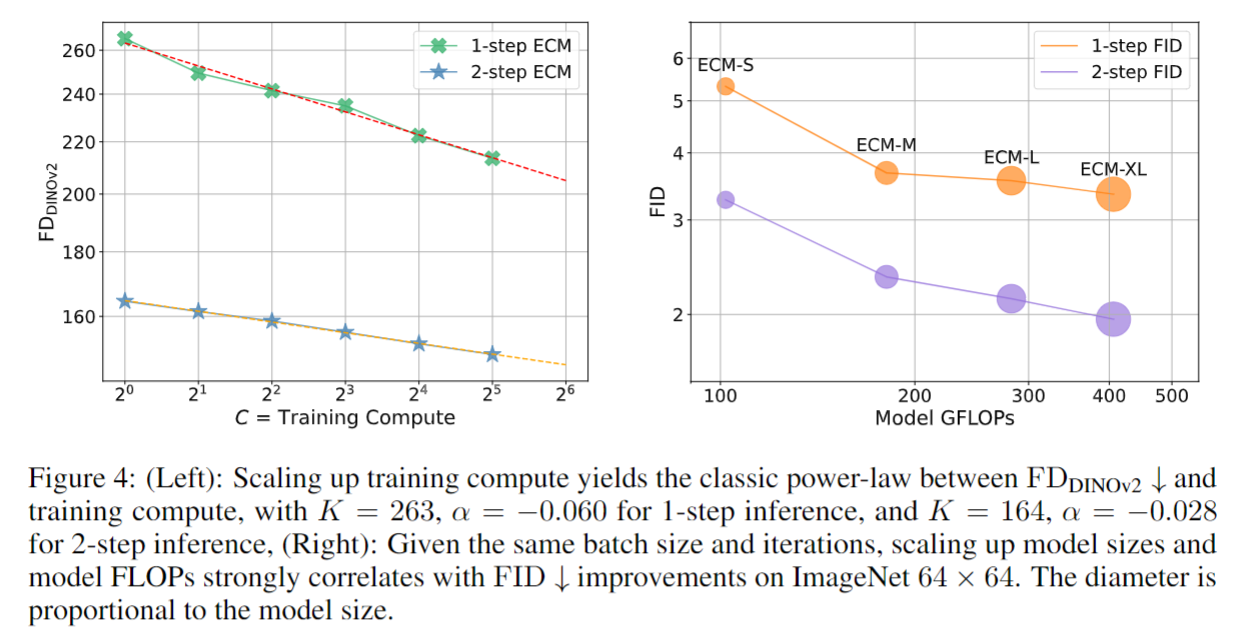
image not found

呈现非常健康的 classic power law.

Limitations

本文提到, 这个 finetune 的方法是 dataset-dependent 的. 现在好像有些 Distillation 不需要数据集. 管

More: Appendix

ECT’s schedule should be adjusted according to the compute budget.

比如想训的少一点, 那么可以直接优化 consistency condition with $\Delta t \sim \text dt$, 能比较快的提升效果. 否则应该慢慢来.

Interesting point: $\text{FD}_{\text {DINOv2}}$

这是一个类似 FID 的东西, 但是使用 DINOv2 作为特征提取模型.

在 eval FID 和 $\text{FD}_{\text {DINOv2}}$ 的时候使用了不同的 dropout (0.2 & 0.3)

更小的模型可以使用稍微小一点的 dropout

  • 不同的 weight function 最优的 dropout 是一样的!

超快训练

在 CIFAR 上, 取 $q=256$, batch size 128, 8000 次 GD, 一个 A100 上面一个小时能训到两部 FID 2.73. 这个弱爆了.

Improvements of techniques on ICM

image not found

Few steps generation

实验表明, 一步法最好的超参和两步法最好的超参是不一样的. 包括 weight function, dropout, EMA rate/length.

比如下面的图片说明了 dropout 的这个性质.

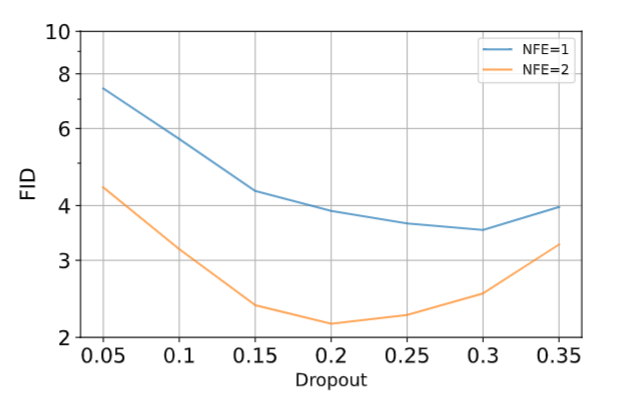
image not found

Training details

见 Appendix D