这篇文章又叫做 ADM (Ablated Diffusion Model).

主要的贡献：

  • unconditional方面，做了一些改动，在Pixel Space上跑了很大的ImageNet (256x256)，并获得了很不错的结果；
  • conditional方面，提出了一种新的方法，叫做 diffusion guidance，可以很不错地完成conditional generation。

Improvements

文章做了一系列的改进，列举如下：

(前面有几点来自于IDDPM这个paper)

  • 原来diffusion 模拟概率分布 $p_\theta(x_{t-1}\mid x_t)=\mathcal{N}(\mu_\theta(x_t,t),\sigma_t)$，并把 $\mu_\theta$ reparameterize成 $\epsilon_\theta$。现在，我们依然保持使用 $\epsilon_\theta$，但是 $\sigma_t$ 不再是固定的数而是一个可学习的
\[\Sigma_\theta(x_t,t) = \exp\left(v_\theta(x_t,t) \log \beta_t + (1-v_\theta(x_t,t))\log \tilde{\beta_t}\right)\]

（注意，这是标量）这里的 $\beta_t$ 就是DDPM里面的，而 $\tilde{\beta_t}=\beta_t\cdot \frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t}$.

  • 我们修改diffusion loss的weight。也就是，
\[L=\sum_t \mathbb{E}_{\tilde{x},\epsilon} \left[\|\epsilon_\theta(\tilde{x},t)-\epsilon\|^2 + \lambda \cdot\frac{d}{2} \left(\log \Sigma_\theta(\tilde{x},t)+\frac{\tilde{\beta_t}}{\Sigma_\theta(\tilde{x},t)}+\frac{\beta_t^2}{\alpha_t(1-\bar{\alpha}_t)\Sigma_\theta(\tilde{x},t)}\|\epsilon_\theta(\tilde{x},t)-\epsilon\|^2\right)\right]\]

这个公式是我自己算的，其实就保证对。但反正他的意思就是，前面这一项保留，后面加上一个KL divergence的项，系数是 $\lambda$.

  • 对模型做的改动其实少，最终结果：
    • 增加attention head的个数有点用
    • 增加attention resolution的个数
    • 使用BigGAN res block
  • AdaGN:
\[\text{AdaGN}(h,y) = y_s\cdot \text{GroupNorm}(h) + y_b\]

其中，$y_s,y_b$ 由time embedding（或者可能是condition embedding）得到。

Classifier Guidance

我们假设有一个noisy image classifier，可以训练出来 $p_\phi(y\mid x_t,t)$。接下来，利用这个classifier的score，我们就可以conditional generation。

其实管数学推导，反正搞出来就是

\[x_{t-1} = \mu_\theta(x_t,t) + s\Sigma_\theta(x_t,t)\log p_\phi(y\mid x_t,t) + \sqrt{\Sigma_\theta(x_t,t)}\epsilon, \quad \epsilon\sim \mathcal{N}(0,I)\]

这是SDE sampler。我们还有DDIM sampler：

\[\hat{\epsilon} = \epsilon_\theta(x_t,t) - \sqrt{1-\bar{\alpha}_t}\nabla \log p_\phi(y\mid x_t,t)\] \[x_{t-1} = \sqrt{\bar{\alpha}_{t-1}}\cdot \frac{x_t-\sqrt{1-\bar{\alpha}_t}\hat{\epsilon}}{\sqrt{\bar{\alpha}_t}}+\sqrt{1-\bar{\alpha}_{t-1}}\hat{\epsilon}\]

classifier的训练和架构都有讲究，这里就不细说了。这个 $s$ 叫做guidance scale，其实就不重要。论文说, $s$ 必须大于1。

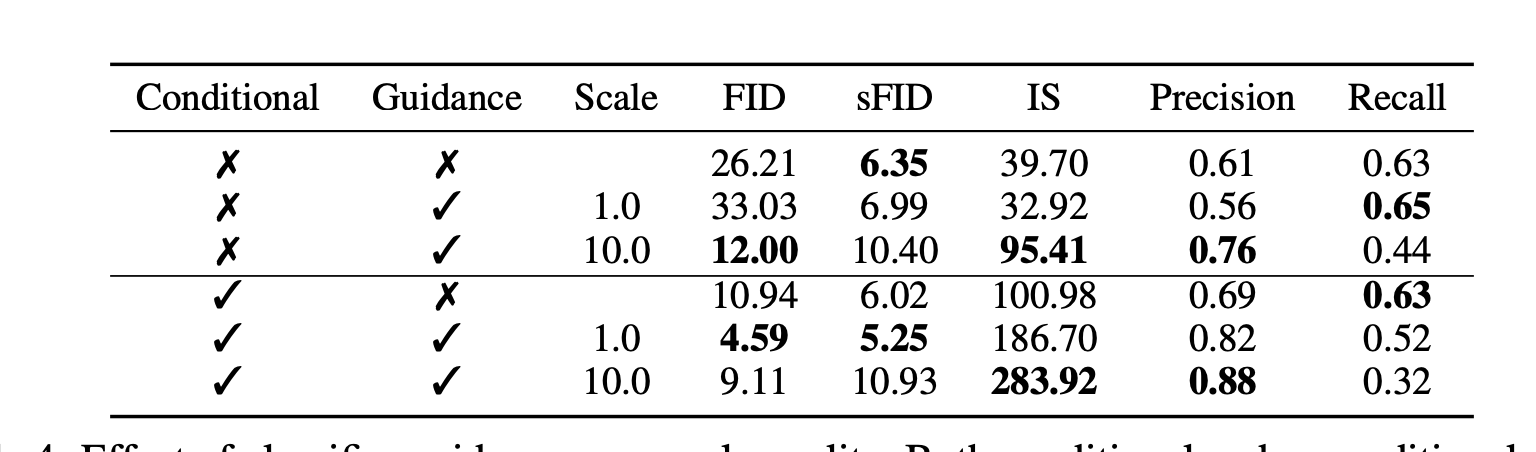
Classifier Guidance v.s. Conditional

我们发现有两种方式：第一种是直接加 class label conditioning，第二种是比较数学的classifier guidance。我们发现，两种都用当然最好，但是如果只能选一个，那还是得用class label conditioning。数学高兴