SQA-007
[Paper] A Connection Between Score Matching and Denoising Autoencoders
Denoising Autoencoder
Given $x$, first corrupt it by adding Gaussian noise $\sigma$, then use an autoencoder. The objective is to minimize the reconstruction error.
An easy model: encoder $h=\text{sigmoid}(W\tilde{x}+b)$, decoder $x’=W^Th+c$, where $\tilde{x}=x+\epsilon$, $\epsilon\sim\mathcal N(0,\sigma^2I)$.
不要问我为什么 encoder 和 decoder 的权重是一样的
Explicit & Implicit Score Matching
记我们的网络是 $\phi(x;\theta)$. The original objective (explicit) \(J_{ESMq}(\theta)=\mathbb E_{q(x)}\left[\frac 12\|\phi(x;\theta)-\nabla_x\log q(x)\|^2\right]\)
但是这个不 tractable. 数学上等价于 implicit objective \(J_{ISMq}(\theta)=\mathbb E_{q(x)}\left[\frac 12\|\phi(x;\theta)\|^2+\nabla\cdot \phi(x;\theta)\right]\) 这样能算了但是有梯度的梯度项.
除此之外, LeCun 还提出了正则项 \(J_{ISMq}(\theta)=\mathbb E_{q(x)}\left[\frac 12\|\phi(x;\theta)\|^2+\nabla\cdot \phi(x;\theta)\right]+\lambda\sum_{i=1}^d \left(\frac{\partial \phi_i(x;\theta)}{\partial x_i}\right)^2\)
Smoothed data
记 $q_{\sigma}$ 表示加 $\sigma$ 的 Gaussian noise 后的分布. 对于这个分布我们可以同样考虑 explicit 和 implicit 的 score matching, 记 training objective 为 $J_{ESMq_{\sigma}}$ 和 $J_{ISMq_{\sigma}}$.
这样我们进一步得到等价的 Denoising Score Matching (DSM) objective \(J_{DSMq_{\sigma}}(\theta)=\mathbb E_{q_{\sigma}(\tilde{x}, x)}\left[\frac 12\|\phi(\tilde{x};\theta)-\nabla_{\tilde{x}}\log q_{\sigma}(\tilde{x}\mid x)\|^2\right]\)
Connection
文中指出, 如果我们有一个 energy model 形如
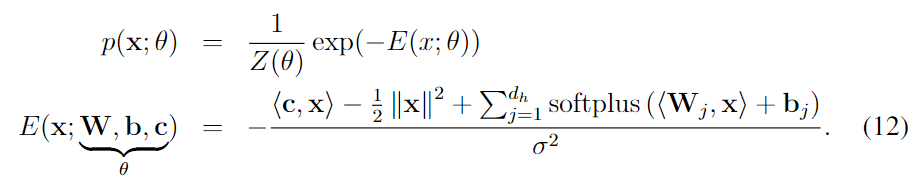 不要问我为什么是这个形式. 看上去后面的项是一个两层MLP, 其中激活函数是 softplus ($x\rightarrow \log(1+\exp(x))$), 而且最后是加起来 (后面好像提到了, 把这层的参数加上也对). 剩下的看上去像是加了一个 linear 然后还有正则项. 最后除以 $\sigma^2$ 相当于温度.
不要问我为什么是这个形式. 看上去后面的项是一个两层MLP, 其中激活函数是 softplus ($x\rightarrow \log(1+\exp(x))$), 而且最后是加起来 (后面好像提到了, 把这层的参数加上也对). 剩下的看上去像是加了一个 linear 然后还有正则项. 最后除以 $\sigma^2$ 相当于温度.
那么对应的 score model 长这样
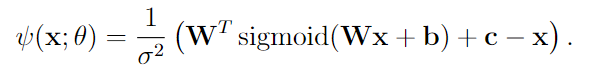
这时候我们对着这个 score model 计算 DSM objective, 发现正好就是 $\frac{1}{2\sigma^4}J_{DAE\sigma}(\theta)$.
这就是他们的 connection.