主要就是把 DiT 换成 FM, 发现能普遍变好, 然后做了不少 ablation

Loss function

我们研究三种 loss, 分别是 unweighted score-matching loss $\mathcal L_s$, $\mathcal L_v$, 还有 weighted score-matching loss

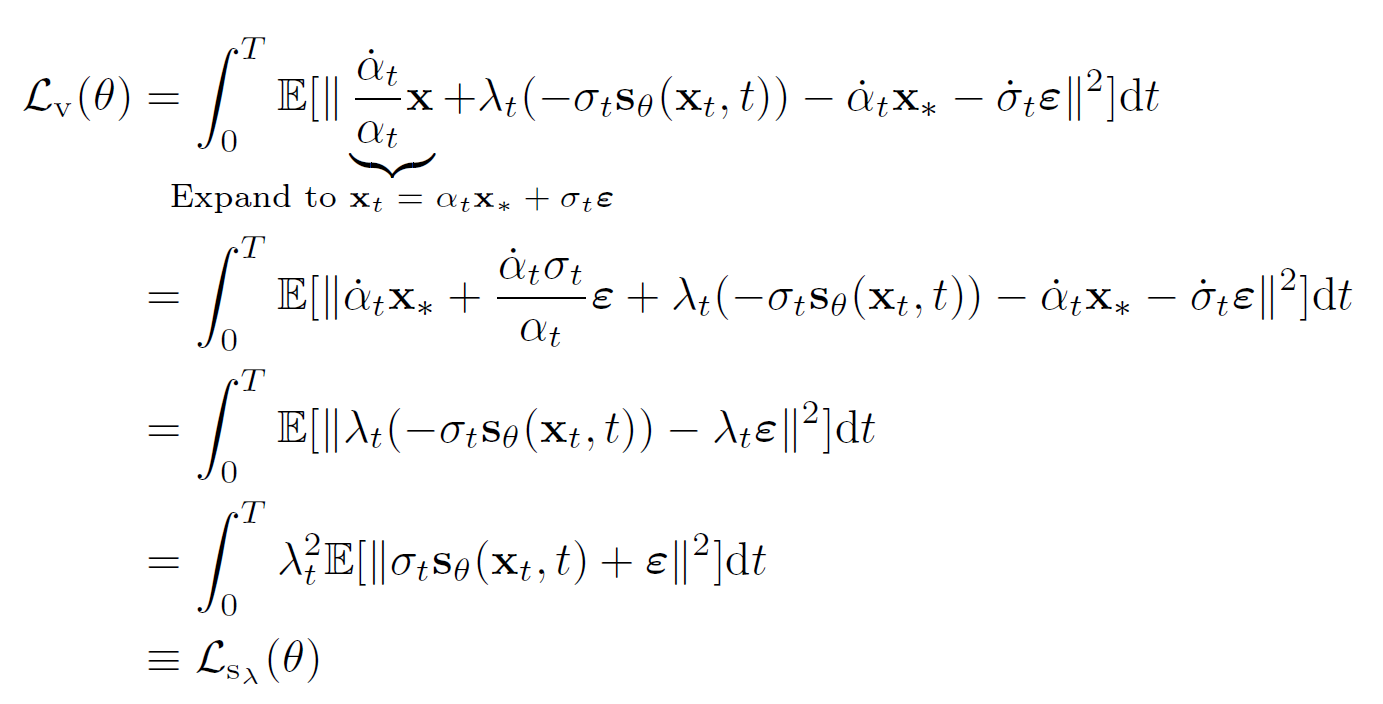
Samplers

我们这里考虑两种 diffusion forward process: $(1-t)x+t\epsilon$ (Linear) 和 $\cos(\frac 1 2 \pi t)x+\sin(\frac 1 2 \pi t)\epsilon$ (GVP, Generalized VP)

General SDE formulation:

\[d x_t = v(x_t, t)dt - \frac 1 2 w_t s(x_t, t)dt + \sqrt{w_t}d\bar{W_t}\]

这里 $w$ 的选取提供了自由度.

Score-based model: $w_t=\beta_t$

提出了更多选择 (动机我79想知道, 反正人家爱怎么解释就怎么解释)

  1. $w_t=\sigma_t$
  2. $w_t=\sin^2(\pi t)$
  3. $w_t=w_t^{KL}=2(\dot{\sigma_t}\sigma_t-\dfrac{\dot{\alpha_t\sigma^2t}}{\alpha_t})$
    这个把 $D    {KL}(p(x)|p_0(x))$ 最小化了
  4. 其中 $L$ 是训练的 MSE loss. 这个唐爆了

Ablations

所有 patch size 全取 2. 卡多就是豪气

  1. Continuous or Discrete time training: 连续的时间更好

  2. Model parameterization: $\mathcal L_v, \mathcal L_{s_{\lambda}}$ 显著更好, 说明 FM 的系数很好

  3. Forward process: Linear / GVP 比经典的 VP 更好. 因为经典的 VP 会导致端点处的 numerical instability

  4. ODE / SDE: SDE 可以比 ODE 更好

  5. Best sampling config:

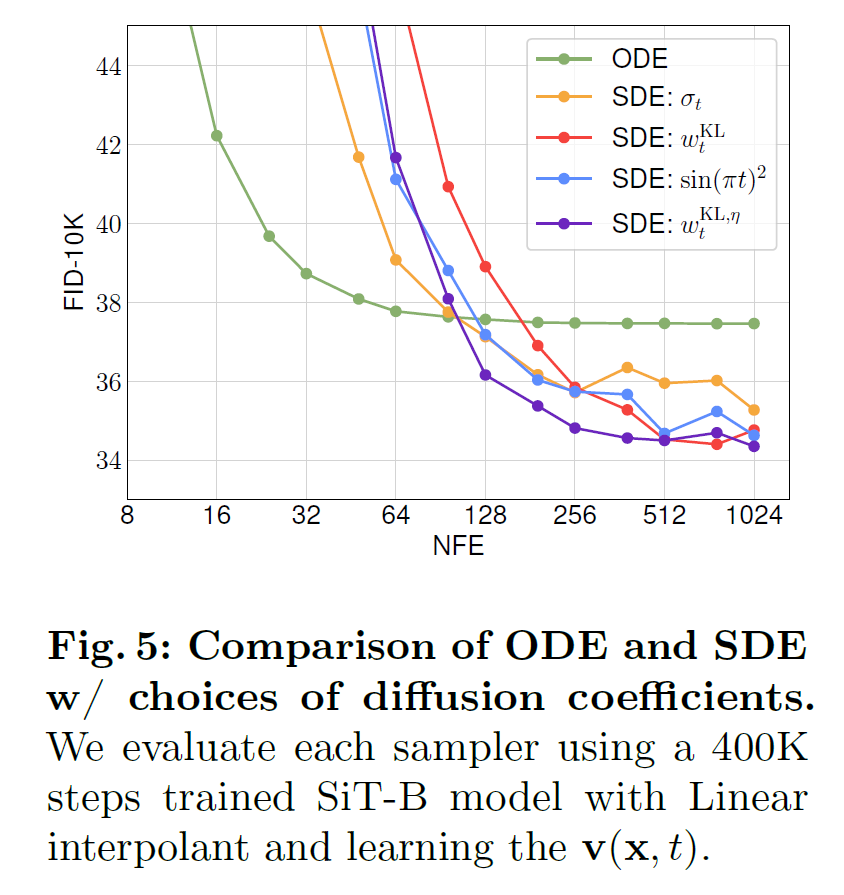
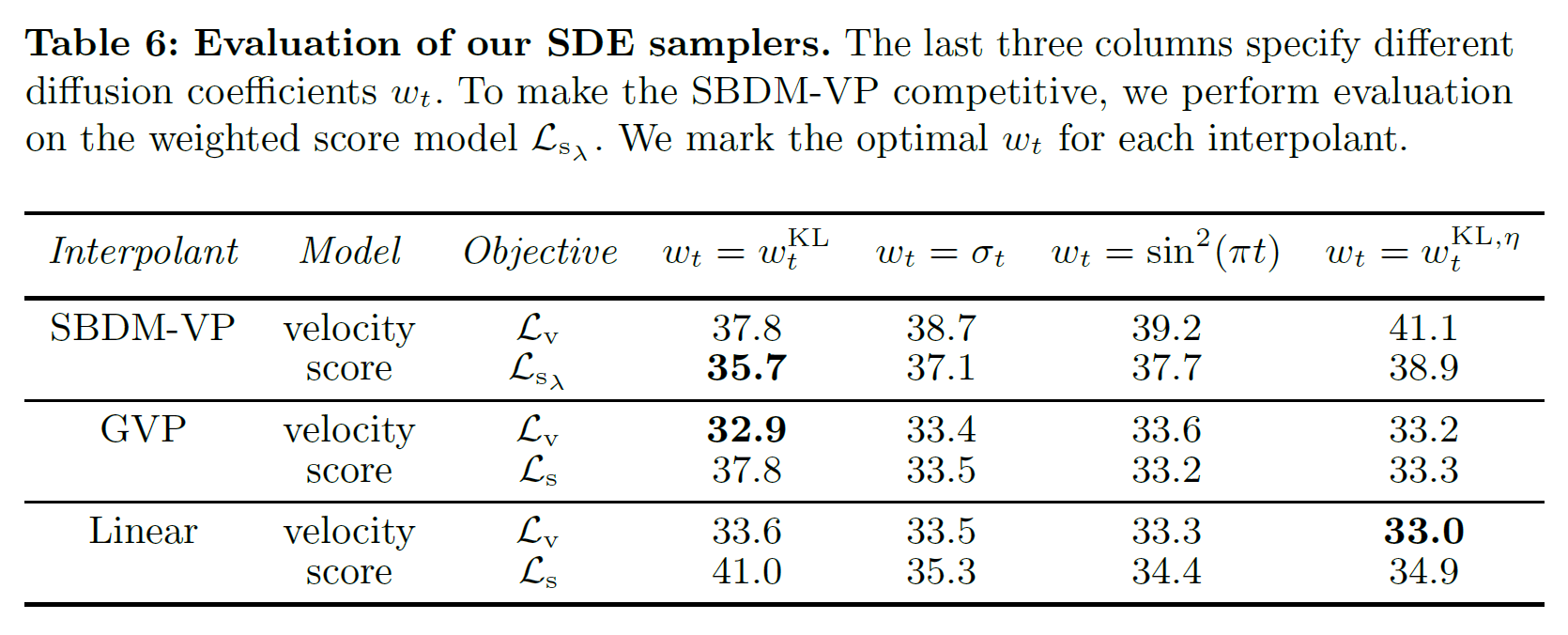
感觉多数想得到, 活一下

对于 XL 来说, 最好的是 Linear + $v$-prediction + $w_t^{KL, \eta}$

Architecture

和 DiT 保持一致, 包括同样的 VAE latent space. 甚至没有调参数

Classifier-free Guidance on velocity field

Simply use $v_{\theta}^{\zeta}(x, t;y)=\zeta v_{\theta}(x, t;y)+ (1-\zeta)v_{\theta}(x, t;\emptyset)$

正好能得到正确的分布

最好的 cfg for XL: 1.5